
【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球。
某校羽毛球队需要购买![]() 副球拍和
副球拍和![]() 盒羽毛球
盒羽毛球![]() .
.
(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含![]() 、
、![]() 的代数式表示;
的代数式表示;
(2)当![]() 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
(3)当![]() 、
、![]() 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
【答案】(1)(270a+36b)(元),(260a+40b)(元); (2)当a=10,b=25时,到甲、乙两家商店购买球拍和羽毛球一样; (3)当a,b满足5a=2b关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同.
【解析】
(1)根据题意可以用代数式分别表示出校羽毛球队在甲、乙两家商店各应花费的钱数;
(2)根据(1)中代数式,将a=10,b=25代入即可解答本题;
(3)根据题意可以得到相应的等式,从而可以得到a、b满足什么条件到甲、乙两家商店购买球拍和羽毛球的费用相同.
(1)由题意可得,
在甲商店购买的费用为:(300a+40b)×0.9=(270a+36b)(元),
在乙商店购买的费用为:300a+40(b![]() a)=(260a+40b)(元);
a)=(260a+40b)(元);
(2)当a=10,b=25时,
在甲商店购买的费用为:270×10+36×25=3600(元),
在乙商店购买的费用为:260×10+40×25=3600(元),
∵3600=3600,
∴当a=10,b=25时,到甲、乙两家商店购买球拍和羽毛球一样;
(3)由题意可得,
(270a+36b)![]() (260a+40b)=0,
(260a+40b)=0,
解得,5a=2b,
答:当a,b满足5a=2b关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
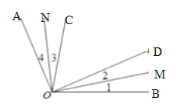
【题目】如图,已知![]() ,
,![]() ,
,![]() 平分
平分![]() ,即
,即![]() ,
,![]() 平分
平分![]() ,即
,即![]() ;
;
![]() 若
若![]() ,则
,则![]() ________;
________;
![]() 若
若![]() 可以在
可以在![]() 内部绕点
内部绕点![]() 作任意旋转(射线
作任意旋转(射线![]() 与射线
与射线![]() 不重合,射线
不重合,射线![]() 与射线
与射线![]() 不重合)则
不重合)则![]() 的大小是否改变?试说明理由.
的大小是否改变?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
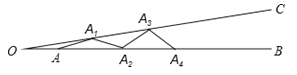
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23﹣6×(﹣3)+2×(﹣4) ; (2)﹣16﹣(﹣5)+23﹣|﹣![]() |
|
(3)﹣(1﹣0.5)÷![]() ×[2+(﹣4)2].
×[2+(﹣4)2].
(4)(4)﹣22﹣(﹣![]() )2×
)2×![]() +6÷|
+6÷|![]() ﹣2|+(﹣1)5×(﹣
﹣2|+(﹣1)5×(﹣![]() )2.
)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() .
.
(1)若A、B移动到如图所示位置,计算![]() 的值.
的值.
(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数![]() ,并计算
,并计算![]() .
.
(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时![]() 比
比![]() 大多少?请列式计算.
大多少?请列式计算.
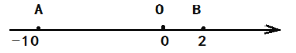
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站相距240千米,从甲站开出一列慢车,速度为每小时80千米,从乙站开出一列快车,速度为每小时120千米.
(1)若两车同时开出,背向而行,则经过多长时间两车相距540千米?
(2)若两车同时开出,同向而行(快车在后),则经过多长时间快车可追上慢车?
(3)若两车同时开出,同向而行(慢车在后),则经过多长时间两车相距300千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
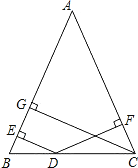
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x﹣5与x轴和y轴分别交于点A和点B,抛物线y=﹣x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.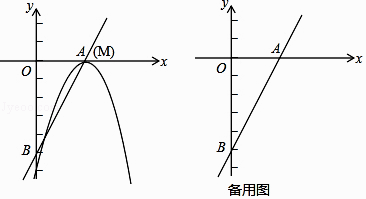
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=﹣x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com