
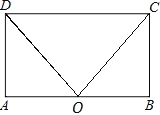
【题目】如图,在平行四边形ABCD中,点O是AB的中点,且OC=OD.
(1)求证:平行四边形ABCD是矩形;
(2)若AD=3,∠COD=60°,求矩形ABCD的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据平行四边形的性质,得出AD=BC,AD∥BC,求出∠A+∠B=180°,根据全等三角形的判定△DAO≌△CBO,根据全等三角形的性质∠A=∠B,求出∠A=90°,根据矩形的判定得出即可;
(2)根据全等求出∠DOA=∠COB,根据勾股定理得出:![]() 求出AO,在球场AB,即可求出面积.
求出AO,在球场AB,即可求出面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠A+∠B=180°,
∵O是AB的中点,
∴AO=BO,
在△DAO和△CBO中
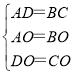
∴△DAO≌△CBO(SSS),
∴∠A=∠B,
∵∠A+∠B=180°,
∴∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
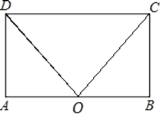
(2)解:∵△DAO≌△CBO,∠DOC=60°,
∴∠DOA=∠COB=![]() (180°-∠DOC)=60°,
(180°-∠DOC)=60°,
∵∠A=90°,
∴∠ADO=30°,
![]() DO=2AO,
DO=2AO,
∵AD=3,
由勾股定理得:![]()
解得:AO=![]() , ∴AB=2AO=
, ∴AB=2AO=![]() ,
,
∴ABCD的面积是AB×AD=![]()


科目:初中数学 来源: 题型:
【题目】为了弘扬二中精神,磨炼学生意志, 4 月14 日下,万州二中初2019级全体师生在学校领导和各班班主任的带领下进行了主题为“放歌平湖之家多美”的环湖拉练活动,师生们从二中初中部出发沿滨江路步行到达三峡移民纪念馆,全体师生在此进行了一个小时左右的宣传与实践活动,然后又乘车返回;设师生所用的时间为x(小时),师生们离开学校的距离为y(千米)则下列各图中,能反映y与x之间关系的图象大致是( )
A. 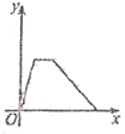 B.
B. 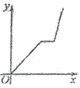 C.
C. 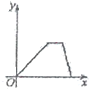 D.
D. 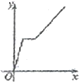
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东同学根据函数的学习经验,对函数y ![]()
![]() 进行了探究,下面是他的探究过程:
进行了探究,下面是他的探究过程:
(1)已知x=-3时![]() 0;x=1 时
0;x=1 时![]() 0,化简:
0,化简:
①当x<-3时,y= ;
②当-3≤x≤1时,y= ;
③当x>1时,y= .
(2)在平面直角坐标系中画出y=|x﹣1|+|x+3|的图象,根据图象,写出该函数的一条性质: ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( )
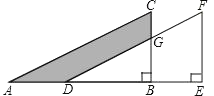
A.12.5B.19.5C.32D.45.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为![]() .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ABCD的两条对角线AC,BD交于点O,点E是CD的中点,△DOE的面积为l0cm2,则△ABD的面积为( )
ABCD的两条对角线AC,BD交于点O,点E是CD的中点,△DOE的面积为l0cm2,则△ABD的面积为( )

A.15cm2B.20cm2C.30cm2D.40cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,作直线
上,作直线![]() ,过点
,过点![]() 作直线
作直线![]() 交直线
交直线![]() 于点
于点![]() .
.
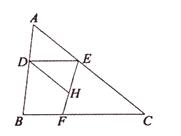
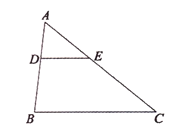
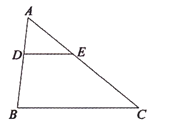
图1 图2 图3
(1)在如图1所示的情况下,求证:![]() ;
;
(2)若三角形![]() 不变,
不变,![]() ,
,![]() 两点的位置也不变,点
两点的位置也不变,点![]() 在直线
在直线![]() 上运动.
上运动.
①当点![]() 在三角形
在三角形![]() 内部时,说明
内部时,说明![]() 与
与![]() 的数量关系:
的数量关系:
②当点![]() 在三角形
在三角形![]() 外部时,①中结论是否依然成立?若不成立,
外部时,①中结论是否依然成立?若不成立,![]() 与
与![]() 又有怎样的数量关系?请在图2中画图探究,并说明理由.
又有怎样的数量关系?请在图2中画图探究,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com