
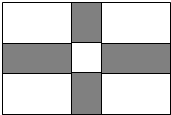
 学校计划用地砖铺设教学楼前的矩形广场ABCD,已知矩形广场的长为100米,宽为60米图案如图所示:广场四角为矩形,阴影部分为矩形,中心为正方形.阴影部分铺设绿色地砖,其余铺设白色地砖.
学校计划用地砖铺设教学楼前的矩形广场ABCD,已知矩形广场的长为100米,宽为60米图案如图所示:广场四角为矩形,阴影部分为矩形,中心为正方形.阴影部分铺设绿色地砖,其余铺设白色地砖.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
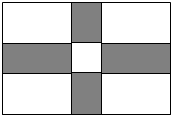 24、学校计划用地砖铺设教学楼前的矩形广场ABCD,已知矩形广场的长为100米,宽为60米图案如图所示:广场四角为矩形,阴影部分为矩形,中心为正方形.阴影部分铺设绿色地砖,其余铺设白色地砖.
24、学校计划用地砖铺设教学楼前的矩形广场ABCD,已知矩形广场的长为100米,宽为60米图案如图所示:广场四角为矩形,阴影部分为矩形,中心为正方形.阴影部分铺设绿色地砖,其余铺设白色地砖.查看答案和解析>>
科目:初中数学 来源: 题型:
 某施工单位计划用地砖铺设正方形广场地面ABCD(如图所示),广场四角白色区域为正方形,阴影部分为四个矩形,四个矩形的宽都等于正方形的边长,阴影部分铺绿色地砖,其余部分铺白色地砖.已知
某施工单位计划用地砖铺设正方形广场地面ABCD(如图所示),广场四角白色区域为正方形,阴影部分为四个矩形,四个矩形的宽都等于正方形的边长,阴影部分铺绿色地砖,其余部分铺白色地砖.已知查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某施工单位计划用地砖铺设正方形广场地面ABCD(如图所示),广场四角白色区域为正方形,阴影部分为四个矩形,四个矩形的宽都等于正方形的边长,阴影部分铺绿色地砖,其余部分铺白色地砖.已知
某施工单位计划用地砖铺设正方形广场地面ABCD(如图所示),广场四角白色区域为正方形,阴影部分为四个矩形,四个矩形的宽都等于正方形的边长,阴影部分铺绿色地砖,其余部分铺白色地砖.已知查看答案和解析>>
科目:初中数学 来源:2011年贵州省贵阳市永乐中学中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com