
分析 (1)分类讨论:当m=0时,方程化为一元一次方程x+3=0,有一个解;当m≠0时,由于△=(3m+1)2-4m×3=(3m-1)2≥0,此时方程有两个实数解,于是可判断不论m为任何实数,此方程总有实数根;
(2)先利用求根公式求出x1=-3,x2=-$\frac{1}{m}$,再利用x12-x22=0得到($\frac{1}{m}$)2=9,然后解关于m的方程即可.
解答 (1)证明:当m=0时,方程化为x+3=0,解得x=-3;
当m≠0时,△=(3m+1)2-4m×3=(3m-1)2≥0,此时方程有两个实数解,
所以不论m为任何实数,此方程总有实数根;
(2)解:x=$\frac{-(3m+1)±(3m-1)}{2m}$,
解得x1=-3,x2=-$\frac{1}{m}$,
∵x12-x22=0,
∴($\frac{1}{m}$)2=9,
∴m=±$\frac{1}{3}$.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.
对(1)个问题要分类讨论.


科目:初中数学 来源: 题型:解答题
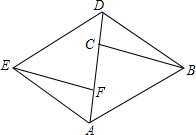 如图,AB∥ED,BC∥EF,点C、点F在AD上,AF=DC.
如图,AB∥ED,BC∥EF,点C、点F在AD上,AF=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com