
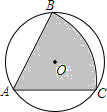
 如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为2π;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$.
如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为2π;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$. 分析 (1)连OA,作OD⊥AC于D,根据垂径定理得到AD=DC,利用含30°的直角三角形三边的关系得到AC=2 $\sqrt{3}$,再利用扇形的面积公式可计算出S阴影部分的面积;
(2)先根据弧长公式计算出弧BC的长,然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长计算该圆锥的底面圆的半径.
解答  解:连OA,作OD⊥AC于D,如图,
解:连OA,作OD⊥AC于D,如图,
则AD=DC,
∵∠BAC=60°,
∴∠OAD=30°,
∴OD=$\frac{1}{2}$OA=$\frac{1}{2}$×2=1,
∴AD=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
∴S阴影部分=$\frac{60π×({2\sqrt{3})}^{2}}{360}$=2π;
(2)∵弧BC的长=$\frac{60π×2\sqrt{3}}{180}$=$\frac{2\sqrt{3}}{3}$π,
∴圆锥的底面圆的半径=$\frac{\frac{2\sqrt{3}π}{3}}{2π}$=$\frac{{\sqrt{3}}}{3}$.
故答案为:2π;$\frac{{\sqrt{3}}}{3}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式和扇形的面积公式.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
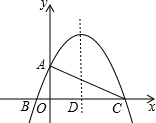 如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
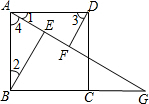 如图,四边形ABCD是边长为4的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
如图,四边形ABCD是边长为4的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com