
�Ķ����в��ϲ���ա�ƽ������n���㣨n��2�������������㲻��ͬһ��ֱ���ϣ�����Щ����ֱ�ߣ�һ����������������ͬ��ֱ�ߣ�
(1
��������������������ʱ��������1��ֱ�ߣ�����3����ʱ��������3��ֱ�ߣ�����4����ʱ��������6��ֱ�ߣ�����5����ʱ��������10��ֱ�ߡ���(2
�����ɣ������ĸ����Ϳ�����ֱ�ߵ�����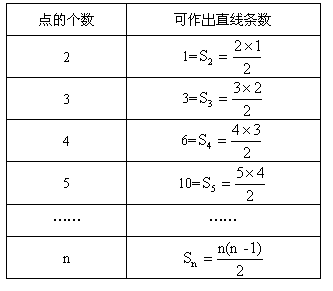
(3)
������ƽ������n���㣬����ȷ��һ��ֱ�ߡ�ȡ��һ����A��n��ȡ����ȡ�ڶ�����B�У�n��1����ȡ��������һ��������n(n-1)��ֱ�ߣ���AB��BA��ͬһ��ֱ�ߣ���Ӧ����2����(4
�����ۣ���̽�����¼������⣺ƽ������n���㣨n��3�������������㲻��ͬһ��ֱ���ϣ��������������������Σ�һ�����������ٲ�ͬ�������Σ�
(1
��������������3����ʱ���������������� ���� �������Σ�
����
������4����ʱ���������������� ���� �������Σ�����
������5����ʱ���������������� ���� �������Σ�����
(2
�����ɣ������ĸ���n�Ϳ������������εĸ���|
��ĸ��� |
������������� |
|
3 |
�� |
|
4 |
�� |
|
5 |
�� |
|
���� |
�� |
|
n |
�� |
(3)
������ ���������������������������� (4�����ۣ� �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| ��ĸ��� | ������ֱ������ | ||
| 2 | 1=S2=
| ||
| 3 | 3=S3=
| ||
| 4 | 6=S4=
| ||
| 5 | 10=S5=
| ||
| �� | �� | ||
| n | Sn=
|
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| ��ĸ��� | �����������θ��� |
| 3 | |
| 4 | |
| 5 | |
| �� | |
| n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| 2��1 |
| 2 |
| 3��2 |
| 2 |
| 4��3 |
| 2 |
| 2��1 |
| 2 |
| 3��2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
���Ķ����в��ϲ���ա�ƽ������n���㣨n��2�������������㲻��ͬһ��ֱ���ϣ�����Щ����ֱ�ߣ�һ����������������ͬ��ֱ�ߣ�
�ٷ�����������������ʱ��������1��ֱ�ߣ�����3����ʱ��������3��ֱ�ߣ�����4����ʱ��������6��ֱ�ߣ�����5����ʱ��������10��ֱ�ߡ���
�ڹ��ɣ������ĸ����Ϳ�����ֱ�ߵ�����![]() ���֣����±�
���֣����±�
| ��ĸ��� | ������ֱ������ |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| ���� | ���� |
| n |
|
��������ƽ������n���㣬����ȷ��һ��ֱ�ߡ�ȡ��һ����A��n��ȡ����ȡ�ڶ�����B�У�n��1����ȡ��������һ��������n(n-1)��ֱ�ߣ���AB��BA��ͬһ��ֱ�ߣ���Ӧ����2����![]()
�ܽ��ۣ�![]()
��̽�����¼������⣺ƽ������n���㣨n��3�������������㲻��ͬһ��ֱ���ϣ��������������������Σ�һ�����������ٲ�ͬ�������Σ�
��1��������
������3����ʱ�������� �������Σ�
������4����ʱ�������� �������Σ�
������5����ʱ�������� �������Σ�
����
��2�����ɣ������ĸ���n�Ϳ������������εĸ���![]() �����֣������±���
�����֣������±���
| ��ĸ��� | �����������θ��� |
| 3 |
|
| 4 |
|
| 5 |
|
| ���� |
|
| n |
|
(3)������
��4�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014���˽̰��һ��һѧ����ĩ������ѧ�� ���ͣ�ѡ����
��1���Ķ����в��ϲ����
�����ⷽ��  +
+ =5
=5
�⣺�� ��x����3ʱ��x+2��0 ��x+3��0��
���� =��x��2��
=��x��2�� =��x��3
=��x��3
����ԭ���̿ɻ�Ϊ ��1�� =5
��� x= ��2��
�� ����3��x ����2ʱ ��x+2��0 ��x+3��0��
���� =-x-2��
=-x-2�� =x+3
=x+3
����ԭ���̿ɻ�Ϊ ��x��2+x+3��5
1��5
���Դ�ʱԭ������
�� ��x�ݣ�2ʱ ��x+2��0 ��x+3��0��
����  = ��3�� ��
= ��3�� �� = ��4��
= ��4��
����ԭ���̿ɻ�Ϊ ��5�� =5
��� x= ��6��
��2��������Ľ��ⷽ���ⷽ��
 ��
�� =x-6
=x-6
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com