
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2的坐标是(2$\sqrt{3}$,4).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2的坐标是(2$\sqrt{3}$,4). 分析 根据题意得出直线AA1的解析式为:y=$\frac{\sqrt{3}}{3}$x+2,进而得出A,A1,A2坐标.
解答 解:过B1向x轴作垂线B1C,垂足为C,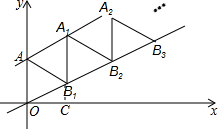
由题意可得:A(0,2),AO∥A1B1,∠B1OC=30°,
∴CO=OB1cos30°=$\sqrt{3}$,
∴B1的横坐标为:$\sqrt{3}$,则A1的横坐标为:$\sqrt{3}$,
连接AA1,可知所有三角形顶点都在直线AA1上,
∵点B1,B2,B3,…都在直线y=$\frac{\sqrt{3}}{3}$x上,AO=2,
∴直线AA1的解析式为:y=$\frac{\sqrt{3}}{3}$x+2,
∴y=$\frac{\sqrt{3}}{3}$×$\sqrt{3}$+2=3,
∴A1($\sqrt{3}$,3),
同理可得出:A2的横坐标为:2$\sqrt{3}$,
∴y=$\frac{\sqrt{3}}{3}$×2$\sqrt{3}$+2=4,
∴A2(2$\sqrt{3}$,4),
故答案为:(2$\sqrt{3}$,4)
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出A点横纵坐标变化规律是解题关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
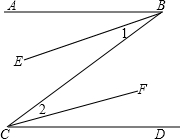 在下面的括号内,填上推理的根据:如图,已知AB∥CD,BE平分∠ABC,CF平分∠BCD,求证:BE∥CF.
在下面的括号内,填上推理的根据:如图,已知AB∥CD,BE平分∠ABC,CF平分∠BCD,求证:BE∥CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一个正方形纸片(图1),切去四个角上同样大小的小正方形,翻折粘合成一个无盖的长方体(图2),若图1中原正方形纸片的边长为6,图2中长方体的长为a,高为b,则下列说法错误的是( )
如图,将一个正方形纸片(图1),切去四个角上同样大小的小正方形,翻折粘合成一个无盖的长方体(图2),若图1中原正方形纸片的边长为6,图2中长方体的长为a,高为b,则下列说法错误的是( )| A. | a<6 | B. | a+2b=6 | ||
| C. | a=2时,图2为正方体 | D. | 长方体的所有棱长之和是个定值 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | t<0 | B. | t=0 | C. | t>0 | D. | t≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com