
【题目】如图,已知A、B两点的坐标分别为(―2,0),(0,1),⊙C的圆心坐标为(0,―1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ) 
A. 4 B. ![]() C.
C. ![]() D. 3
D. 3
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,一条自南向北的大道上有O、A两个景点,O、A相距20km,在O处测得另一景点C位于点O的北偏东37°方向,在A处测得景点C位于点A的南偏东76°方向,且A、C相距13km .
(1)求:①A到OC之间的距离;
②O、C两景点之间的距离;
(2)若在O处测得景点B 位于景点O的正东方向10km,求B、C两景点之间的距离.(参考数据:tan37°=0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.
(1)孔明同学调查的这组学生共有_______人;
(2)这组数据的众数是_____元,中位数是_____元;
(3)若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的弦,C为弦AB上一点,设AC=m,BC=n(m>n),将弦AB绕圆心O旋转一周,若线段BC扫过的面积为(m2﹣n2)π,则![]() =_____.
=_____.
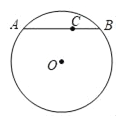
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若AB=2,BC=4,求⊙O的半径.
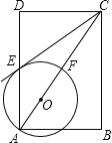
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某我市花石镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:
(1)设装运A种湘莲的车辆数为x,装运B种湘莲的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
湘莲品种 | A | B | C |
每辆汽车运载量(吨) | 12 | 10 | 8 |
每吨湘莲获利(万元) | 3 | 4 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com