
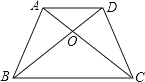
【题目】在梯形ABCD中,AD//BC,下列条件中,不能判断梯形ABCD是等腰梯形的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】A、∵∠ABC=∠DCB,∴AB=DC,
∵AD∥BC,∴四边形ABCD是等腰梯形,故本选项正确,不符合题意;
B、∵AD//BC,∴∠ADB=∠DBC,∠DAC=∠ACB,∵∠DBC=∠ACB,
∴OB=OC,∠DAC=∠ADB,∴OA=OD,
∴OA+OC=OB+OD,即AC=BD,∴梯形ABCD是等腰梯形,故本选项正确,不符合题意;
C、∵AD//BC,∴∠ADB=∠DBC,∠DAC=∠ACB,
∵∠DAC=∠DBC,∴∠ACB=∠DBC,∠ADB=∠DAC,
∴OB=OC,OA=OD,
∴OA+OC=OB+OD,即AC=BD,∴梯形ABCD是等腰梯形,故本选项正确,不符合题意;
D、根据![]() ,只能推出AD=CD,再根据AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误,符合题意,
,只能推出AD=CD,再根据AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误,符合题意,
故选D.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).

(1)当x为何值时,PQ∥BC;
(2)当△APQ与△CQB相似时,AP的长为________.;
(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个产品销售点在经销某著名特色小吃时发现:如果每箱产品赢利10元,每天可销售50箱,若每箱产品涨价1元,日销量将减少2箱.
(1)现该销售点为使每天赢利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元?才能使每天的盈利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=7,AC=6,∠A=45°,点D、E分别在边AB、BC上,将△BDE沿着DE所在直线翻折,点B落在点P处,PD、PE分别交边AC于点M、N,如果AD=2,PD⊥AB,垂足为点D,那么MN的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
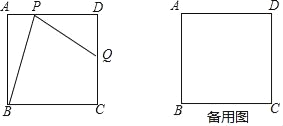
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中, ![]() ,
, ![]() ,△CDE中,
,△CDE中, ![]() ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若![]() 三点共线,
三点共线, ![]() 为
为![]() 中点.
中点.
①直接指出![]() 与
与![]() 的关系______________;
的关系______________;
②直接指出![]() 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕![]() 点逆时针旋转
点逆时针旋转![]() (如图2,
(如图2, ![]() ),试确定
),试确定![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若![]() ,请直接指出点
,请直接指出点![]() 所经历的路径长.
所经历的路径长.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣3与2x﹣1成正比例,且当x=1时,y=6.
(1)求y与x之间的函数解析式.
(2)当x=2时,求y的值.
(3)若点A(x1,y1),B(x2,y2)都在该函数的图象上,且y1>y2,试判断x1,x2的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com