
 ��ͼ����֪�����ϵ�A��ʾ����Ϊ6��B��������λ�ڵ�A���һ�㣬��AB=22��
��ͼ����֪�����ϵ�A��ʾ����Ϊ6��B��������λ�ڵ�A���һ�㣬��AB=22������ ��1��������֪�ɵ�B���ʾ����Ϊ6-22��
��2����P�˶�x��ʱ���ڵ�C���ϵ�Q����AC=5x��BC=3x���г�����ʽ��ɣ�
�ٵ���P�ڵ�A��B����֮���˶�ʱ���ڵ���P�˶�����B�����ʱ�������е�Ķ�����߶εĺͲ����MN�ij����ɣ�
��� �⣺��1���ߵ�A��ʾ����Ϊ6��B��A����ߣ�AB=22��
���B��ʾ������6-22=-16��
�ʴ�Ϊ��-16��
��2����PA=5t��BQ=3t��
�ڵ���P��Q����֮ǰʱ��������ɵã�3t+2+5t=22��
��ã�t=2.5��
����P��Q����֮��ʱ��������ɵã�3t-2+5t=22��
��ã�t=3��
����2.5��3��ʱ��P��Q֮��ľ���ǡ�õ���2��
��PA=5t=30��
MN=MP-NP=$\frac{1}{2}AP-\frac{1}{2}BP=\frac{1}{2}��30-\frac{1}{2}��30-22��=11$��
�ʴ�Ϊ��5t��3t��30
���� ���⿼��������һԪһ�η��̵�Ӧ�ã��õ���֪ʶ��������������֮��ľ��룬�ؼ��Ǹ������⻭��ͼ�Σ�ע�����������������ۣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
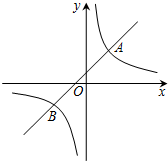 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��ͼ����A��2��3����B��-3��n�����㣮
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��ͼ����A��2��3����B��-3��n�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
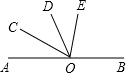 ��ͼ����֪OΪֱ��AB��һ�㣬OCƽ�֡�AOD����BOD=3��DOE����COE=�������BOE�Ķ�����
��ͼ����֪OΪֱ��AB��һ�㣬OCƽ�֡�AOD����BOD=3��DOE����COE=�������BOE�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
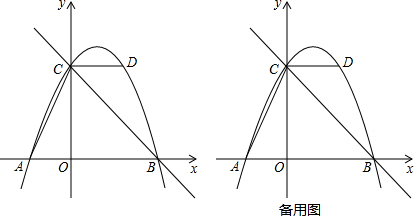
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{1}{2}$x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����x=-$\frac{3}{2}$�Ҿ���A��C���㣬��x�����һ����Ϊ��B������BC��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{1}{2}$x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����x=-$\frac{3}{2}$�Ҿ���A��C���㣬��x�����һ����Ϊ��B������BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
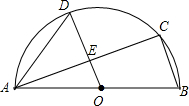 ��ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E��
��ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com