
分析 (1)如图1,根据三角形的内角和得到∠A=30°,根据直角三角形的性质得到BC=$\frac{1}{2}$AB,于是得到结论;
(2)正确,如图2,取AB的中点D,连接CD,由线段中点的定义得到BD=AD=$\frac{1}{2}$AB,等量代换得到BC=BD,推出∠BCD=∠BDC=60°,根据等腰三角形和外角的性质得到∠A=∠ACD=$\frac{1}{2}∠$BDC=30°,即可得到结论;
(3)分两种情况考虑:(i)当PQ⊥BC时,如图所示,由速度是1厘米/秒,时间是t秒,利用速度×时间=路程表示出AP与BQ的长,再由AB-AP表示BP,由三角形ABC为等边三角形,得到∠B=60°,在直角三角形BPQ中,利用锐角三角函数定义及特殊角的三角函数值列出关于t的方程,求出方程的解即可得到t的值;(ii)当QP⊥AB时,如图所示,由速度是1厘米/秒,时间是t秒,利用速度×时间=路程表示出AP与BQ的长,再由AB-AP表示BP,由三角形ABC为等边三角形,得到∠B=60°,在直角三角形BPQ中,利用锐角三角函数定义及特殊角的三角函数值列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
解答  解:(1)上述结论1正确,
解:(1)上述结论1正确,
如图1,∵∠C=90°,∠B=60°,
∴∠A=30°,
∴BC=$\frac{1}{2}$AB,
∴60°内角的两夹边长是2倍的关系;
故答案为:正确;
(2)正确,如图2,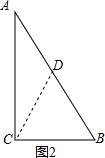 取AB的中点D,连接CD,
取AB的中点D,连接CD,
∴BD=AD=$\frac{1}{2}$AB,
∵BC=$\frac{1}{2}$AB,
∴BC=BD,
∵∠B=60°,
∴△BDC是等边三角形,
∴∠BCD=∠BDC=60°,
∵AD=CD,
∴∠A=∠ACD=$\frac{1}{2}∠$BDC=30°,
∴∠ACB=90°,
∴在一个三角形中,如果60°内角的两夹边长是2倍的关系,那么这个三角形是直角三角形正确.
(3)分两种情况考虑:
(i)当PQ⊥BC时,如图3所示:
由题意可得:AP=BQ=t,BP=4-t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=$\frac{BQ}{BP}$=$\frac{1}{2}$,即$\frac{t}{4-t}$=$\frac{1}{2}$,
解得:t=$\frac{4}{3}$秒;
(ii)当QP⊥AB时,如图4所示:
由题意可得:AP=BQ=t,BP=4-t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=$\frac{BP}{BQ}$=$\frac{1}{2}$,即$\frac{4-t}{t}$=$\frac{1}{2}$,
解得:t=$\frac{8}{3}$秒,
综上所述,t的值是$\frac{4}{3}$秒或$\frac{8}{3}$秒.
点评 此题考查了含30°角的直角三角形的性质,等边三角形的性质,锐角三角函数定义,特殊角的三角函数值,利用了分类讨论及方程的思想,熟练掌握等边三角形的性质是解本题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
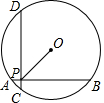 如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
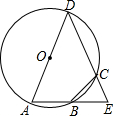 如图,以△ADE的边AD为直径的⊙O交AE于B,交DE于C,$\widehat{AB}$=$\widehat{BC}$,求证:BC=BE.
如图,以△ADE的边AD为直径的⊙O交AE于B,交DE于C,$\widehat{AB}$=$\widehat{BC}$,求证:BC=BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com