
 如图,C是线段AB上的一点,D是线段BC的中点,已知图中所有线段的长度之和为23.5,线段AC的长度与线段BC的长度都是正整数,则线段AC的长为2.
如图,C是线段AB上的一点,D是线段BC的中点,已知图中所有线段的长度之和为23.5,线段AC的长度与线段BC的长度都是正整数,则线段AC的长为2. 分析 可以设出AC和CD的长,再根据图中所有线段的长度之和为23,即可列出等式,再根据线段AC的长度与线段CB的长度都是正整数,即可求出答案.
解答 解:设AC=y,CD=BD=x,则AC+CD+DB+AD+AB+CB=23,
即:y+x+x+(x+y)+(2x+y)+2x=23,
得:7x+3y=23.5,
因为线段AC的长度与线段CB的长度都是正整数,
所以可知x最大为3,
可知:x=3,y为小数,不符合;
x=2.5,y=2
x=2,y为小数,不符合;
x=1.5,y为小数,不符合
x=1,y为小数,不符合,
x=0.5y为小数,不符合.
所以AC=2,
故答案为:2.
点评 本题考查了比较线段长短的知识,有一定难度,根据题意列出方程式,并探讨解的合理性是关键.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
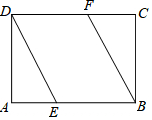 如图,E、F分别是矩形ABCD的边AB、CD上一点,且AE=CF,连接BF、DE.
如图,E、F分别是矩形ABCD的边AB、CD上一点,且AE=CF,连接BF、DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
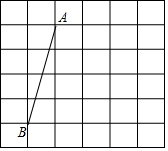 如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.
如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com