
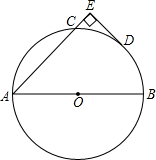
 如图,AB为⊙O直径,D为BC弧的中点,DE⊥AC于E,
如图,AB为⊙O直径,D为BC弧的中点,DE⊥AC于E,分析 (1)要证明DE是⊙O的切线只要证明OD⊥DE即可;
(2)证明四边形DECF是矩形得出CE=DF=2,CF=DE=4,设⊙O的半径为r,则OF=r-2,在Rt△OBF中,由勾股定理得出方程,解方程即可.
解答 (1)证明:连接OD、BC交于点F,如图所示:
∵D为弧BC的中点,
∴OD⊥BC,
∵AB为直径,
∴∠ACB=90°,
又∵DE⊥AC,
∴∠CED=∠ECF=∠CFD=90°,
∴∠FDE=90°,即OD⊥DE,
又∵OD为⊙O的半径,
∴DE是⊙O的切线;
(2)解:∵OD⊥BC,
∴BF=CF,
∵∠CED=∠ECF=∠CFD=90°,
∴四边形DECF是矩形,
∴CE=DF=2,CF=DE=4,
设⊙O的半径为r,则OF=r-2,
在Rt△OBF中,由勾股定理得:(r-2)2+42=r2,
解得:r=5,
即⊙O的半径为5.
点评 本题考查了切线的判定、圆周角定理、矩形的判定与性质、勾股定理;熟练掌握切线的判定,由勾股定理得出方程是解决问题(2)的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com