
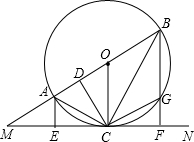
 已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.
已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.分析 ①由MN与圆O相切于点C,根据弦切角定理可得∠ACE=∠ABC,又由AB为圆O直径,可得AC⊥BC,则可证得Rt△AEC≌Rt△ADC,同理可得Rt△BCD≌Rt△BCF,根据全等三角形的对应边相等,即可得CD=CF=CE;
②由①可证得Rt△ACE∽Rt△CBF,根据相似三角形的对应边成比例,与CE=CF=$\frac{1}{2}$EF,即可证得EF2=4AE•BF;
③由Rt△BCD≌Rt△BCF与Rt△ACE≌Rt△GCF即可证得AD•DB=FG•FB;
④由△AME∽△CMD与Rt△ACD∽Rt△BCF.利用相似三角形的对应边成比例,即可求得MC•CF=MA•BF.
解答 解:∵MN与圆O相切于点C,
∴∠ACE=∠ABC,
又∵AB为圆O直径,
∴AC⊥BC,
∵CD⊥AB,
∴∠ABC=90°-∠BAC=90°-∠DAC=∠ACD,
∴∠ACE=∠ACD,
∵∠AEC=∠ADC=90°,
在Rt△AEC和Rt△ADC中,
$\left\{\begin{array}{l}{∠AEC=∠ADC}\\{∠ACE=∠ACD}\\{AC=AC}\end{array}\right.$,
∴Rt△AEC≌Rt△ADC(AAS),
∴CD=CE,
同理,Rt△BCD≌Rt△BCF,
∴CD=CE=CF,
故①正确;
由①的过程知:∠ACE=∠DBC=∠FBC,
∵∠AEC=∠CFB=90°,
∴Rt△ACE∽Rt△CBF,
∴$\frac{AE}{CF}$=$\frac{CE}{BF}$,
∴CE•CF=AE•BF,
由①的结论知,CE=CF=$\frac{1}{2}$EF,
∴$\frac{1}{4}$EF2=AE•BF
∴EF2=4AE•BF,
故②正确;
由①过程知,Rt△BCD≌Rt△BCF
∴DB=FB,…(1)
∵MN为⊙O切线,
∴∠FCG=∠FBC=∠ABC=∠ACE,
由①结论知,CE=CF,
∵∠AEC=∠GFC=90°,
在Rt△ACE和Rt△GCF中,
$\left\{\begin{array}{l}{∠AEC=∠GFC}\\{CE=CF}\\{∠ACE=∠FCG}\end{array}\right.$,
∴Rt△ACE≌Rt△GCF(ASA),
而由①的过程知,Rt△ACE≌Rt△ACD,
∴Rt△ACD≌Rt△GCF,
∴AD=FG,…(2)
由(1)(2)得到:AD•DB=FG•FB;
故③正确;
∵∠M=∠M,∠AEM=∠ADC,
∴△AME∽△CMD,
∴$\frac{MC}{DC}=\frac{MA}{AE}$,
∵AE=AD,
∴$\frac{MC}{DC}=\frac{MA}{DA}$,
∴$\frac{CM}{DC}=\frac{CD}{DA}$,…(3)
又∵Rt△ACD∽Rt△BCF,
∴$\frac{DC}{DA}=\frac{BF}{CF}$,…(4)
由(3)(4)得到:$\frac{MC}{MA}=\frac{BF}{CF}$,
∴MC•CF=MA•BF;
故④正确,
故答案为:①②③④.
点评 此题考查了圆周角定理,切线的性质,相似三角形与全等三角形的判定与性质等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想的应用,注意比例的性质.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
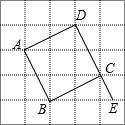 如图,在5×5的正方形网格中,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,延长DC与过点B的水平网格线交于点E,则线段CE的长为$\frac{\sqrt{5}}{2}$.
如图,在5×5的正方形网格中,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,延长DC与过点B的水平网格线交于点E,则线段CE的长为$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
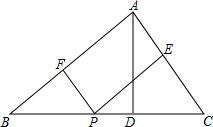 在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.
在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)
已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
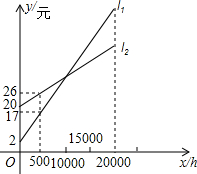 如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,
如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com