
【题目】如图1,在圆O中,直径CD⊥弦AB于点E,点P是CD延长线上一点,连接PB、BD.

(1)若BD平分∠ABP,求证:PB是圆O的切线;
(2)若PB是圆O的切线,AB=4,OP=4,求OE的长;
(3)如图2,连接AP,延长BD交AP于点F,若BD⊥AP,AB=2![]() ,OP=4,求tan∠BDE的值.
,OP=4,求tan∠BDE的值.
【答案】(1)见解析;(2)OE=2;(3)tan∠BDE=![]() .
.
【解析】
(1)连接BC,BO,根据圆周角定理得到∠CBD=90°,根据等腰三角形的性质得到∠OBC=∠C,于是得到结论;
(2)设OB=r,OE=x,证△OBE∽△OPB得![]() ,即r2=4x,在Rt△OBE中,由OB2=OE2+BE2可得关于x的方程,解之可得答案;
,即r2=4x,在Rt△OBE中,由OB2=OE2+BE2可得关于x的方程,解之可得答案;
(3)连接BC,BO,根据已知条件得到AP∥BC,根据平行线的性质得到∠C=∠APC,根据垂径定理得到AE=BE,根据等腰三角形的性质得到CE=PE,设OE=x,CO=BO=r,根据勾股定理即可得到x的值,进一步可得DE的长,根据三角函数的定义可得答案.
解:(1)连接BC,BO,

∵CD是⊙O的直径,
∴∠CBD=90°,
∵CD⊥AB,
∴∠DBE=∠C=90°﹣∠CDB,
∵OB=OC,
∴∠OBC=∠C,
∵∠PBD=∠EBD,
∴∠PBD=∠OBC,
∴∠PBO=90°,
∴PB是⊙O的切线;
(2)设OB=r,OE=x,
∵PB为⊙O的切线,CD⊥AB,
∴∠OBP=∠OEB=90°,
又∵∠BOE=∠POB,
∴△OBE∽△OPB,
则![]() ,即
,即![]() ,
,
∴r2=4x,
∵AB=4,CD⊥AB,
∴AE=BE=2,
在Rt△OBE中,由OB2=OE2+BE2可得4x=x2+4,
解得:x=2,即OE=2;
(3)如图2,连接BC,BO,
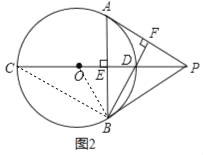
∵CD是⊙O的直径,
∴BC⊥BD,
∵BD⊥AP,
∴AP∥BC,
∴∠C=∠APC,
∵CD是⊙O的直径,CD⊥AB,
∴AE=BE,
∴AP=BP,
∴∠APC=∠BPC,
∴∠C=∠BPC,
∴CE=PE,
设OE=x,CO=BO=r,
∴r+x=4﹣x,
∴r=4﹣2x,
∵AB=2![]() ,
,
∴BE=![]() AB=
AB=![]() ,
,
在Rt△BEO中,BO2=OE2+BE2,即(4﹣2x)2=x2+(![]() )2,
)2,
解得:x=1或x=![]() (不合题意,舍去),
(不合题意,舍去),
∴OE=1、OD=OB=4﹣2=2,
则DE=OD﹣OE=1,
∴tan∠BDE=![]() =
=![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
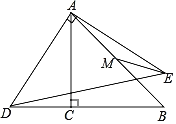
【题目】如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D与点A(0,6)、B(0,﹣4)、C(x,y)是平行四边形的四个顶点,其中x、y满3x﹣4y+12=0,则CD的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A、B 两点,交 y 轴于 C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论:①abc>0;②4a﹣2b+c>0;③5a+2c>3b;④(4a﹣b)(2a+b)<0;正确的有( )个.
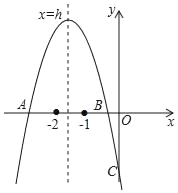
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表8.
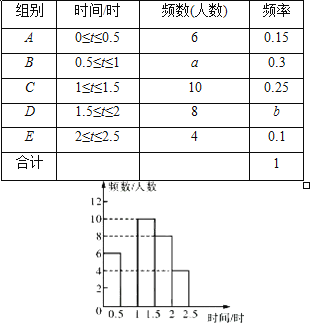
请根据图表中的信息,解答下列问题:
(1)表中的a=______,b=______,中位数落在________组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作读书心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
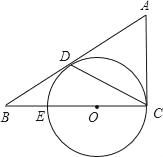
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
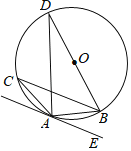
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的布袋中装有1个红球,2个白球,它们除颜色外其余完全相同.
(1)从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个白球的概率;
(2)若在布袋中再添加a个白球,充分搅匀,从中摸出一个球,使摸到红球的概率为![]() ,试求a的值.
,试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com