
分析 根据非负数的性质列出方程组,根据高次方程的解法求出x、y的值,计算即可.
解答 解:由题意得,$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}-4=0①}\\{3\sqrt{5}x-5y-10=0②}\end{array}\right.$,
由②得,y=$\frac{3\sqrt{5}}{5}$x-2③,
把③代入①得,x2-3$\sqrt{5}$x+10=0,
解得,x1=$\sqrt{5}$,x2=2$\sqrt{5}$,
把x1=$\sqrt{5}$,x2=2$\sqrt{5}$代入③,得y1=1,y2=4,
则xy=$\sqrt{5}$或8$\sqrt{5}$.
故答案为:$\sqrt{5}$或8$\sqrt{5}$.
点评 本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.


科目:初中数学 来源: 题型:解答题
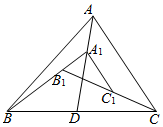 如图,在△ABC中,BD=DC,AA1=$\frac{1}{3}$AD,A1B1=$\frac{1}{3}$A1B,B1C1=C1C,△A1B1C1面积为1平方厘米,则△ABC的面积为多少平方厘米?
如图,在△ABC中,BD=DC,AA1=$\frac{1}{3}$AD,A1B1=$\frac{1}{3}$A1B,B1C1=C1C,△A1B1C1面积为1平方厘米,则△ABC的面积为多少平方厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
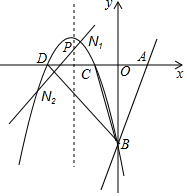 如图所示,直线l:y=3x-3与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,抛物线过点B,C和D(-3,0).
如图所示,直线l:y=3x-3与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,抛物线过点B,C和D(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com