
【题目】某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的![]() 倍,购进数量比第一次少了25本.
倍,购进数量比第一次少了25本.
(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读资料,解决问题.
人教版《数学九年级(下册)》的![]() 页有这样一个思考问题:
页有这样一个思考问题:
问题:如图,在![]() 中,
中,![]() 交
交![]() ,
,![]() 于点
于点![]() ,
,![]() ,如果通过“相似的定义”证明
,如果通过“相似的定义”证明![]() ?
?
根据“两直线平行,同位角相等”容易得出三对对应角分别相等,再根据“平行线分线段成比例”的基本事实,容易得出![]() ,所以这个问题的核心时如何证明“
,所以这个问题的核心时如何证明“![]() ”.
”.
证明思路:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,构造平行四边形
,构造平行四边形![]() ,得到
,得到![]() ,从而将比例式中的
,从而将比例式中的![]() ,
,![]() 转化为共线的两条线段
转化为共线的两条线段![]() ,
,![]() ,同时也构造了基本图形“
,同时也构造了基本图形“ ”,得到
”,得到![]() ,从而得证.
,从而得证.

解决问题:
(![]() )①类比资料中的证明思路,请你证明“三角形内角平分线定理”.
)①类比资料中的证明思路,请你证明“三角形内角平分线定理”.
三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图![]() ,
,![]() 中,
中,![]() 是角平分线.
是角平分线.
求证:![]() .
.

②运用“三角形内角平分线定理”填空:
已知:如图![]() ,
,![]() 中,
中,![]() 是角平分线,
是角平分线,![]() ,
,![]() ,
,![]() ,则
,则![]() __________.
__________.
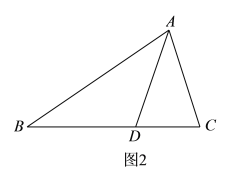
(![]() )我们知道,如果两个三角形有相同的高或者相等的高,那么它们面积的比就等于底的比.
)我们知道,如果两个三角形有相同的高或者相等的高,那么它们面积的比就等于底的比.
请你通过研究![]() 和
和![]() 面积的比来证明三角形内角平分线定理.
面积的比来证明三角形内角平分线定理.
已知:如图![]() ,
,![]() 中,
中,![]() 是角平分线.
是角平分线.
求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 以每秒1个单位的速度从点
以每秒1个单位的速度从点![]() 出发运动到点
出发运动到点![]() ,点
,点![]() 以相同的速度从点
以相同的速度从点![]() 出发运动到点
出发运动到点![]() ,两点同时出发,过点
,两点同时出发,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
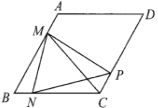
(1)当![]() 和
和![]() 时,请你分别在备用图1,备用图2中画出符合题意的图形;
时,请你分别在备用图1,备用图2中画出符合题意的图形;
(2)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)当点![]() 在线段
在线段![]() 的延长线上时,是否存在某一时刻
的延长线上时,是否存在某一时刻![]() 使
使![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后,点
顺时针旋转一定角度后,点![]() 的对应点恰好与点
的对应点恰好与点![]() 重合,得到
重合,得到![]() .
.

(1)请求出旋转角的度数;
(2)请判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若![]() ,
,![]() ,试求出四边形
,试求出四边形![]() 的对角线
的对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b,当x=2时,y=﹣3,当x=1时,y=﹣1.
(1)求一次函数的解析式;
(2)若该一次函数的图形交x轴y轴分别于A、B两点,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的![]() ;
;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com