
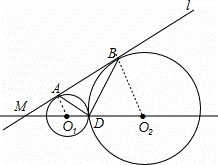
如图,⊙O1与⊙O2外切与点D,直线l与两圆分别相切于点A、B,与直线
O1、O2相交于点M,且tan∠AM01=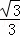 ,MD=4
,MD=4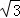 .
.
(1)求⊙O2的半径;
(2)求△ADB内切圆的面积;
(3)在直线l上是否存在点P,使△MO2P相似于△MDB?若存在,求出PO2的长;若不存在,请 说明理由.
说明理由.
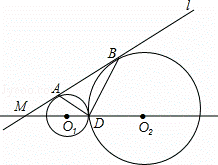
解:(1)连结O1A、O2B,如图,设⊙O1的半径为r,⊙O2的半径为R,
∵⊙O1与⊙O2外切与点D,
∴直线O1O2过点D,
∴MO2=MD+O2D=4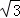 +R,
+R,
∵直线l与两圆分别相切于点A、B,
∴O1A⊥AB,O2B⊥AB,
∵tan∠AM01=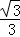 ,
,
∴∠AM01=30°,
在Rt△MBO2中,MO2=O2B=2R,
∴4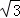 +R=2R,解得R=4
+R=2R,解得R=4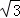 ,
,
即⊙O2的半径为4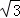 ;
;
(2)∵∠AM02=30°,
∴∠MO2B=60°,
而O2B=O2D,
∴△O2BD为等边三角形,
∴BD=O2B=4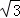 ,∠DBO2=60°,
,∠DBO2=60°,
∴∠ABD=30°,
∵∠AM01=30°,
∴∠MO1A=60°,
而O1A=O1D,
∴∠O1AD=∠O1DA,
∴∠O1AD=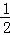 ∠MO1A=30°,
∠MO1A=30°,
∴∠DAB=60°,
∴∠ADB=180°﹣30°﹣60°=90°,
在Rt△ABD中,AD=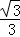 BD=4,AB=2AD=8,
BD=4,AB=2AD=8,
∴△ADB内切圆的半径=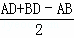 =
=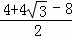 =2
=2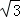 ﹣2,
﹣2,
∴△ADB内切圆的面积=π•(2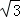 ﹣2)2=(16﹣8
﹣2)2=(16﹣8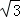 )π;
)π;
(3)存在.
在Rt△MBO2中,MB=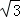 O2B=
O2B=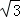 ×4
×4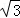 =12,
=12,
当△MO2P∽△MDB时,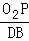 =
=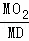 ,即
,即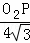 =
=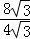 ,解得O2P=8
,解得O2P=8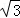 ;
;
当△MO2P∽△MBD时,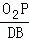 =
=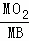 ,即
,即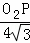 =
=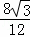 ,解得O2P=8,
,解得O2P=8,
综上所述,满足条件的O2P的长为8或8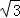 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
某校枇杷基地的枇杷成熟了,准备请专业摘果队帮忙摘果,现有甲、乙两支专业摘果队,若由甲队单独摘果,预计6填才能完成,为了减少枇杷因气候变化等原因带来的损失,现决定由甲、乙两队同时摘果,则2填可以完成,请问:
(1)若单独由乙队摘果,需要几天才能完成?
(2)若有三种摘果方案,方案1:单独请甲队;方案2:同时请甲、乙两队;方案3:单独请乙对.甲队每摘果一天,需支付给甲队1000元工资,乙队每摘果一天,须支付给乙队1600元工资,你认为用哪种方案完成所有摘果任务需支付给摘果队的总工资最低?最低总工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
某服装厂接到一份加工3000件服装的订单.应客户要求,需提前供货,该服装厂决定提高加工速度,实际每天加工的件数是原计划的1.5倍,结果提前10天完工.原计划每天加工多少件服装?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com