
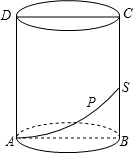
 如图,圆柱的轴截面ABCD是边长为4的正方形,一动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为多少?(用π表示)
如图,圆柱的轴截面ABCD是边长为4的正方形,一动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为多少?(用π表示) 科目:初中数学 来源: 题型:填空题
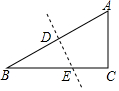 如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=4cm,现将△ABC沿直线DE翻折,使点A和点B重合,则折痕DE长为$\sqrt{5}$cm.
如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=4cm,现将△ABC沿直线DE翻折,使点A和点B重合,则折痕DE长为$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
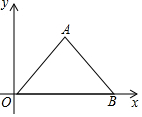 如图,在平面直角坐标系中,△AOB为等腰直角三角形A(4,4),点C从O出发,以2个单位/秒的速度沿x轴正方向运动.
如图,在平面直角坐标系中,△AOB为等腰直角三角形A(4,4),点C从O出发,以2个单位/秒的速度沿x轴正方向运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
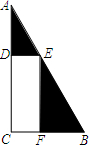 王大伯准备在一块直角三角形菜地上开辟出一块矩形菜地种植菠菜,剩余菜地种植白菜,如图.已知∠ACB=90°,AB=50m,种植菠菜的矩形菜地CDEF的另3个顶点分别在AC,AB,BC上,设CD的长度为x m,矩形CDEF的面积为y m2.
王大伯准备在一块直角三角形菜地上开辟出一块矩形菜地种植菠菜,剩余菜地种植白菜,如图.已知∠ACB=90°,AB=50m,种植菠菜的矩形菜地CDEF的另3个顶点分别在AC,AB,BC上,设CD的长度为x m,矩形CDEF的面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com