
【答案】1.1×107。
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】将11000000用科学记数法表示为:1.1×107.
故答案为:1.1×107.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年贵州省遵义市中考数学真题试卷(解析版).doc 题型:解答题
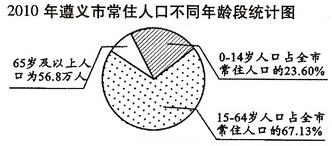
第六次全国人口普查工作圆满结束,2011年5月20日《遵义晚报》报到了遵义市人口普查结果,并根据我市常住人口情况,绘制出不同年龄的扇形统计图;普查结果显示,2010年我市常住人口中,每10万人就有4402人具有大学文化程度,与2000年第五次人口普查相比,是2000年每10万人具有大学文化程度人数的3倍少473人,请根据以上信息,【答案】下列问题.
(1)65岁及以上人口占全市常住人口的百分比是 9.27% ;
(2)我市2010年常住人口约为 612.7 万人(结果保留四个有效数字);
(3)与2000年我市常住人口654.4万人相比,10年间我市常住人口减少 41.67 万人;
(4)2010年我市每10万人口中具有大学文化程度人数比2000年增加了多少人?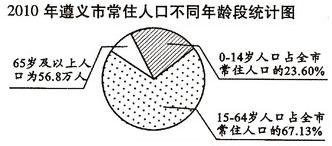
查看答案和解析>>
科目:初中数学 来源: 题型:
为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?

【解题思路】(1)分别观察折线和扇形图不合格的1瓶占甲的10%,所以甲被抽取了10瓶,已被抽取了:18-10=8瓶。
(2)结合两图及问题(1)得乙优秀的瓶数共![]() 瓶,所以优秀率为
瓶,所以优秀率为![]()
【答案】
⑴(由不合格瓶数为1知道甲不合格的瓶数为1)甲、乙分别被抽取了10瓶、8瓶
⑵P(优秀)=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【解题思路】(1)如下表
| 甲(s) 乙(t) | 红桃3 | 红桃4 | 黑桃5 |
| 红桃3 |
|
|
|
| 红桃4 |
|
|
|
| 黑桃5 |
|
|
|
由上表可知:︱s-t︱≥1的概率= ![]() =
=![]() (也可画树形图求解)。
(也可画树形图求解)。
(2)方案A:如表
| 甲(花色) 乙(花色) | 红桃3 | 红桃4 | 黑桃5 |
| 红桃3 | 同色 | 同色 | 不同色 |
| 红桃4 | 同色 | 同色 | 不同色 |
| 黑桃5 | 不同色 | 不同色 | 同色 |
由上表可得![]()
方案B:如表
| 甲 乙 | 红桃3 | 红桃4 | 黑桃5 |
| 红桃3 | 3+3=6 | 3+4=7 | 3+5=8 |
| 红桃4 | 4+3=7 | 4+4=8 | 4+5=9 |
| 黑桃5 | 5+3=8 | 5+4=9 | 5+5=10 |
由上表可得![]()
因为![]() ,所以选择A方案甲的胜率更高.
,所以选择A方案甲的胜率更高.
【答案】⑴![]() ⑵A方案
⑵A方案![]() ,B方案
,B方案![]() ,故选择A方案甲的胜率更高.
,故选择A方案甲的胜率更高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【答案】14![]() 。
。
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =
=![]() =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =
=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=![]() =
=![]() =14
=14![]() .
.
故答案为:14![]() .
.
【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com