
【题目】如图,在Rt△ABC中,∠C=90°,BC=4![]() ,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
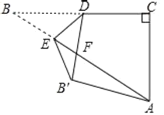
【答案】![]()
【解析】
作EH⊥AB′交AB′的延长线于H.设AE=x.证明Rt△ADC≌Rt△ADB′(HL),得出AC=AB′=4,在Rt△EHB′中,B′H=![]() B′E=
B′E=![]() (8-x),EH=
(8-x),EH=![]() B′H=
B′H=
![]() (8-x),在Rt△AEH中,由勾股定理得出方程,解方程即可.
(8-x),在Rt△AEH中,由勾股定理得出方程,解方程即可.
解:作EH⊥AB′交AB′的延长线于H,连接AD.设AE=x.
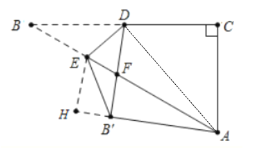
在Rt△ABC中,,BC=4![]() ,AC=4,∴AB=8,tanB=
,AC=4,∴AB=8,tanB=![]() =
=![]()
∴∠B=30°.
∵点D是BC的中点,∴BD=DC
由折叠的性质,得BD= DB′.
∴CD=DB′,
∵AD=AD,
∴Rt△ADC≌Rt△ADB′(HL),
∴AC=AB′=4,
∵∠AB′E=∠AB′F+∠EB′F=90°+30°=120°,
∴∠EB′H=60°,
在Rt△EHB′中,B′H=![]() B′E=
B′E=![]() (8-x),EH=
(8-x),EH=![]() B′H
B′H
![]() (8-x),
(8-x),
在Rt△AEH中,∵EH2+AH2=AE2,
∴[![]() (8-x)]2+[4+
(8-x)]2+[4+![]() (8-x)]2=x2,
(8-x)]2=x2,
解得:x=![]() .
.


科目:初中数学 来源: 题型:
【题目】今年疫情期间,为防止疫惰扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有_______人:在扇形统计图中,表示“微信”的扇形圆心角的度数为_______;其它沟通方式所占的百分比为_______;
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.①请估计最喜欢用“微信”进行沟通的人数:并:用科学计数法表示;②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
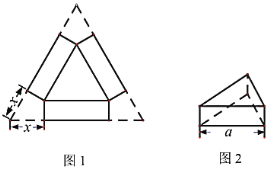
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求该家具商场计划购进的餐桌、餐椅的进价分别为多少元?
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD交CD的延长线于点E,DA平分∠BDE.
⑴求证:AE是⊙O的切线;
⑵若AE=4cm,CD=6cm,求AD的长.
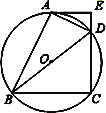
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com