
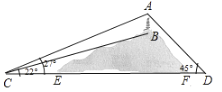
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.

(1)试判断FG与⊙O的位置关系,并说明理由;
(2)若AC=6,CD=5,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
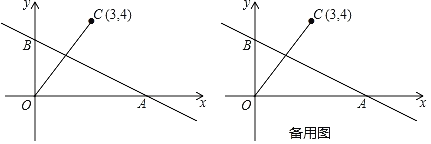
【题目】如图,Rt△OAB的直角边OA在x轴上,边OB在y轴上,A的坐标为(6,0),B的坐标为(0,3),在第一象限有一点C的坐标为(3,4).
(1)求直线AB的函数表达式;
(2)P是x轴上一动点,点P在运动过程中,是否存在某个位置,使得∠PBO=∠BOC?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若动点P在x轴上从点(﹣6,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.请直接写出当t为何值时,在直线l上存在点M,在直线AB上存在点Q.使得以OC为一边,O,C,M,Q为顶点的四边形为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调査结果绘制成的统计图(部分)如图

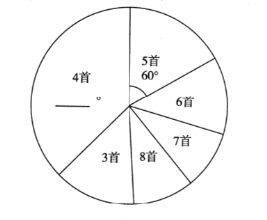
大赛结束后一个月,再次抽查这部分学生的周诗词诵背数量,绘制成如下统计表:
诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息分析
(1)学校团委一共抽取了多少名学生进行调查
(2)大赛前诵背4首人数所在扇形的圆心角为 ,并补充完条形统计图
(3)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
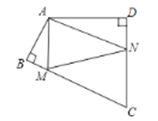
A.140°B.130°C.120°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
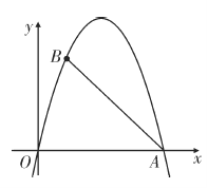
【题目】如图,抛物线![]() 过坐标原点和
过坐标原点和![]() ,
,![]() 两点.
两点.
(1)求该抛物线的表达式;
(2)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出点
两部分?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
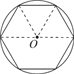
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈![]() =
=![]() =3,那么当n=12时,π≈
=3,那么当n=12时,π≈![]() ≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com