Question

3．已知关于x的方程x²+2（m-1）x+m²-2m=0．
（1）求证：无论m取何值时，方程总有两个不相等的实数根；
（2）抛物线y=x²+2（m-1）x+m²-2m与x轴交于A（x₁，0），B（x₂，0）两点，且x₁＜0＜x₂，抛物线的顶点为C，求△ABC的面积；
（3）在（2）的条件下，若m是整数，记抛物线在点B，C之间的部分为图象G（包含B，C两点），点D是图象G上的一个动点，点P是直线y=2x+b上的一个动点，若线段DP的最小值是$\frac{{\sqrt{5}}}{5}$，请直接写出b的值．

Answer 1

分析 （1）将数据代入△=b²-4ac中得出△=4＞0，从而证出结论成立；
（2）令抛物线解析式中y=0，解关于x的一元二次方程得出方程的根，由此得出线段AB的长度，再令x=-$\frac{b}{2a}$，找出顶点C的纵坐标，结合三角形的面积公式即可得出结论；
（3）结合（2）得出m的值，从而得出点A、B、C三点的坐标，分两种情况考虑b的值．①直线的图象在图象G的上方，通过求直线BC的解析式找出点C到直线y=2x+b的距离最短，通过构建直角三角形，利用勾股定理即可找出关于b的一元一次方程，解方程即可求出b值；②直线的图象在图象G的下方，可得出点B到直线的距离最短，通过构建直角三角形，利用勾股定理即可找出关于b的一元一次方程，解方程即可求出b值．综合两种情况即可得出结论．

解答 （1）证明：∵a=1，b=2（m-1），c=m²-2m，
∴△=b²-4ac=4（m-1）²-4（m²-2m）=4＞0，
∴无论m取任何实数时，方程总有两个不相等的实数根．
（2）解：令抛物线解析式y=x²+2（m-1）x+m²-2m中y=0，则x²+2（m-1）x+m²-2m=（x+m）（x+m-2）=0，
解得：x=-m或x=-m+2，
∵x₁＜0＜x₂，
∴x₁=-m，x₂=-m+2，
∴AB=2．
当x=-$\frac{b}{2a}$=-m+1时，y=-1，
∴y_c=-1，
∴${S_{△ABC}}=\frac{1}{2}AB×|{y_c}|=1$．
（3）解：∵-m＜0＜-m+2，且m为整数，
∴m=1，
即抛物线的解析式为y=x²-1．
∴点B（1，0），点A（-1，0），点C（0，-1）．
直线y=2x+b分两种情况：
①直线y=2x+b的图象在图象G的上方，连接BC，如图1所示．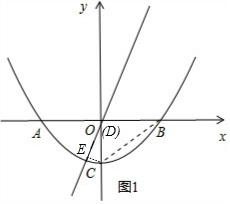

设线段BC所在的直线为y=kx+c，
∵点C（0，-1），点B（1，0）在直线BC上，
∴有$\left\{\begin{array}{l}{-1=c}\\{0=k+c}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=1}\\{c=-1}\end{array}\right.$．
∴直线BC的解析式为y=x-1，
∴点C到直线y=2x+b的距离最近，且为$\frac{\sqrt{5}}{5}$，在图1中，过点C作CE⊥直线y=2x+b于点E，
直线y=2x+b于y轴交于点D（0，b），DC=b-（-1）=b+1，
在Rt△DCE中，DE=2CE，CE=$\frac{\sqrt{5}}{5}$，
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=b+1=1，
解得：b=0；
②直线y=2x+b的图象在图象G的下方，过点B作BF⊥直线y=2x+b于点F，如图2所示．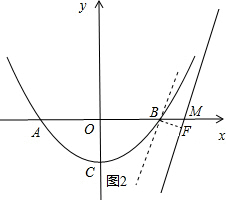

直线y=2x+b与x轴交于点M（-$\frac{b}{2}$，0），
∴BM=-$\frac{b}{2}$-1，
在Rt△BMF中，BF=$\frac{\sqrt{5}}{5}$，MF=$\frac{1}{2}$BF=$\frac{\sqrt{5}}{10}$，
∴BM=$\sqrt{B{F}^{2}+M{F}^{2}}$=-$\frac{b}{2}$-1=$\frac{1}{2}$，
解得：b=-3．
综上可知：若线段DP的最小值是$\frac{{\sqrt{5}}}{5}$，则b的值为0或-3．

点评 本题考查了根的判别式、三角形的面积公式、解一元二次方程以及点到直线的距离，解题的关键是：（1）根据根的判别式的符号确定根的个数；（2）找出线段AB的长度；（3）分两种情况考虑直线的位置．本题属于中档题，难道不大，解决该题型题目时，判断出哪点到直线的距离最短是关键．