
·ÖĪö £Ø1£©ĄūÓĆĶźČ«Ę½·½¹«Ź½·Ö½āµĆ³ö¼“æÉ£»
£Ø2£©Ź×ĻČ½«µŚŅ»”¢Čż”¢ĖÄĻī×éŗĻ£¬ĄūÓĆĶźČ«Ę½·½¹«Ź½·Ö½āŅņŹ½£¬½ų¶ųĄūÓĆĘ½·½²ī¹«Ź½·Ö½āŅņŹ½µĆ³ö¼“æÉ£»
£Ø3£©Ź×ĻČ½«µŚŅ»”¢ĖÄĻīŅŌ¼°µŚ¶ž”¢ČżĻī×éŗĻ£¬½ų¶ųĢįČ”¹«ŅņŹ½·Ø·Ö½āŅņŹ½£¬¼“æÉµĆ³öa£¬b£¬cµÄ¹ŲĻµ£¬ÅŠ¶ĻČż½ĒŠĪŠĪד¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©x2+2xy+y2=£Øx+y£©2£»
£Ø2£©a2-9-2ab+b2
=£Øa-b£©2-32
=£Øa-b+3£©£Øa-b-3£©£»
£Ø3£©”ßa2-4bc+4ac-ab=0£¬
a2-ab+4ac-4bc=0£¬
”ąa£Øa-b£©+4c£Øa-b£©=0£¬
”ą£Øa-b£©£Øa+4c£©=0£¬
”ßa+4c£¾0£¬
”ąa-b=0£¬
”ąa=b£¬
”ą”÷ABCµÄŠĪדŹĒµČŃüČż½ĒŠĪ£®
µćĘĄ “ĖĢāÖ÷ŅŖæ¼²éĮĖ·Ö×é·Ö½ā·Ø·Ö½āŅņŹ½ŅŌ¼°µČŃüČż½ĒŠĪµÄÅŠ¶Ø£¬ÕżČ··Ö×é·Ö½āµĆ³öŹĒ½āĢā¹Ų¼ü£®


 øßÖŠ±ŲĖ¢ĢāĻµĮŠ“š°ø
øßÖŠ±ŲĖ¢ĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ¼×”¢ŅŅĮ½ČĖĄūÓĆ²»Ķ¬µÄ½»Ķع¤¾ß£¬ŃŲĶ¬Ņ»Ā·Ļß“ÓAµŲ³ö·¢Ē°ĶłBµŲ£¬¼×³ö·¢1hŗó£¬ŅŅ³ö·¢£¬Į½ČĖµ½“ļBµŲŗóĮ¢æĢ°“ŌĖŁ¶Č·µ»Ų£¬Éč¼×ÓėAµŲĻą¾ąy¼×£Økm£©£¬ŅŅÓėAµŲĻą¾ąyŅŅ£Økm£©£¬¼×ĄėæŖAµŲµÄŹ±¼äĪŖx£Øh£©£¬y¼×”¢yŅŅÓėxÖ®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®
¼×”¢ŅŅĮ½ČĖĄūÓĆ²»Ķ¬µÄ½»Ķع¤¾ß£¬ŃŲĶ¬Ņ»Ā·Ļß“ÓAµŲ³ö·¢Ē°ĶłBµŲ£¬¼×³ö·¢1hŗó£¬ŅŅ³ö·¢£¬Į½ČĖµ½“ļBµŲŗóĮ¢æĢ°“ŌĖŁ¶Č·µ»Ų£¬Éč¼×ÓėAµŲĻą¾ąy¼×£Økm£©£¬ŅŅÓėAµŲĻą¾ąyŅŅ£Økm£©£¬¼×ĄėæŖAµŲµÄŹ±¼äĪŖx£Øh£©£¬y¼×”¢yŅŅÓėxÖ®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | +3 | B£® | 0 | C£® | -3 | D£® | -6 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1øö | B£® | 2øö | C£® | 3øö | D£® | 4øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
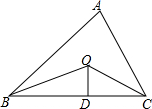 ČēĶ¼£¬ŅŃÖŖ”÷ABCµÄÖܳ¤ŹĒ21£¬OB£¬OC·Ö±šĘ½·Ö”ĻABCŗĶ”ĻACB£¬OD”ĶBCÓŚ£¬ĒŅOD=4£¬”÷ABCµÄĆ껿ŹĒ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖ”÷ABCµÄÖܳ¤ŹĒ21£¬OB£¬OC·Ö±šĘ½·Ö”ĻABCŗĶ”ĻACB£¬OD”ĶBCÓŚ£¬ĒŅOD=4£¬”÷ABCµÄĆ껿ŹĒ£Ø””””£©| A£® | 25 | B£® | 84 | C£® | 42 | D£® | 21 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | a-3£¼b-3 | B£® | 3-a£¼3-b | C£® | $\frac{1}{3}$a£¼$\frac{1}{3}$b | D£® | -2a£¾-2b |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com