
°æƒø°ø∂®“£∫
˝—ߪÓ∂ØøŒ…œ£¨¿Ó¿œ ¶∏¯≥ˆ»Áœ¬∂®“£∫»Áπ˚“ª∏ˆ»˝Ω«–Œ”–“ª±þ…œµƒ÷–œþµ»”⁄’‚Ãı±þµƒ“ª∞Σ¨ƒ«√¥≥∆’‚∏ˆ»˝Ω«–ŒŒ™°∞÷«ª€»˝Ω«–Œ°±£Æ
¿ÌΩ‚£∫
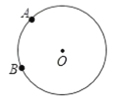
£®1£©»ÁÕº£¨“—÷™![]() °¢
°¢![]() «
«![]() …œ¡Ωµ„£¨«Î‘⁄‘≤…œ’“≥ˆ¬˙◊„Ãıº˛µƒµ„
…œ¡Ωµ„£¨«Î‘⁄‘≤…œ’“≥ˆ¬˙◊„Ãıº˛µƒµ„![]() £¨ π
£¨ π![]() Œ™°∞÷«ª€»˝Ω«–Œ°±£®ª≠≥ˆµ„
Œ™°∞÷«ª€»˝Ω«–Œ°±£®ª≠≥ˆµ„![]() µƒŒª÷√£¨±£¡Ù◊˜Õº∫€º££©£ª
µƒŒª÷√£¨±£¡Ù◊˜Õº∫€º££©£ª
£®2£©»ÁÕº£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨
÷–£¨![]() «
«![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨![]() «
«![]() …œ“ªµ„£¨«“
…œ“ªµ„£¨«“![]() £¨ ‘≈–∂œ
£¨ ‘≈–∂œ![]() «∑ÒŒ™°∞÷«ª€»˝Ω«–Œ°±£¨≤¢Àµ√˜¿Ì”…£ª
«∑ÒŒ™°∞÷«ª€»˝Ω«–Œ°±£¨≤¢Àµ√˜¿Ì”…£ª
‘À”√£∫
£®3£©»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨
÷–£¨![]() µƒ∞Îæ∂Œ™1£¨µ„
µƒ∞Îæ∂Œ™1£¨µ„![]() «÷±œþ
«÷±œþ![]() …œµƒ“ªµ„£¨»Ù‘⁄
…œµƒ“ªµ„£¨»Ù‘⁄![]() …œ¥Ê‘⁄“ªµ„
…œ¥Ê‘⁄“ªµ„![]() £¨ πµ√
£¨ πµ√![]() Œ™°∞÷«ª€»˝Ω«–Œ°±£¨µ±∆‰√ʪ˝»°µ√◊Ó–°÷µ ±£¨÷±Ω”–¥≥ˆ¥À ±µ„
Œ™°∞÷«ª€»˝Ω«–Œ°±£¨µ±∆‰√ʪ˝»°µ√◊Ó–°÷µ ±£¨÷±Ω”–¥≥ˆ¥À ±µ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©![]() «∑ÒŒ™°∞÷«ª€»˝Ω«–Œ°±£¨¿Ì”…º˚Ω‚Œˆ£ª£®3£©µ„
«∑ÒŒ™°∞÷«ª€»˝Ω«–Œ°±£¨¿Ì”…º˚Ω‚Œˆ£ª£®3£©µ„![]() µƒ◊¯±Í
µƒ◊¯±Í £¨
£¨ £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©¡¨Ω·AO≤¢«“—”≥§Ωª‘≤”⁄C1£¨¡¨Ω·BO≤¢«“—”≥§Ωª‘≤”⁄C2£¨º¥ø…«ÛΩ‚£ª
£®2£©…Ë’˝∑Ω–Œµƒ±þ≥§Œ™4a£¨±Ì æ≥ˆDF°¢CF“‘º∞EC°¢BEµƒ≥§£¨»ª∫Û∏˘æðπ¥π…∂®¿Ì¡– Ω±Ì æ≥ˆAF2°¢EF2°¢AE2£¨‘Ÿ∏˘æðπ¥π…∂®¿ÌƒÊ∂®¿Ì≈–∂®°˜AEF «÷±Ω«»˝Ω«–Œ£¨”…÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√°˜AEFŒ™°∞÷«ª€»˝Ω«–Œ°±£ª
£®3£©∏˘æð°∞÷«ª€»˝Ω«–Œ°±µƒ∂®“Âø…µ√°˜OPQŒ™÷±Ω«»˝Ω«–Œ£¨∏˘æð“‚ø…µ√“ªÃı÷±Ω«±þŒ™1£¨µ±–±±þ◊Ó∂à ±£¨¡Ì“ªÃı÷±Ω«±þ◊Ó∂㨑Ú√ʪ˝»°µ√◊Ó–°÷µ£¨”…¥πœþ∂Œ◊Ó∂Ãø…µ√–±±þ◊Ó∂ÃŒ™3£¨∏˘æðπ¥π…∂®¿Ìø…«Û¡Ì“ªÃı÷±Ω«±þ£¨‘Ÿ∏˘æð»˝Ω«–Œ√ʪ˝ø…«Û–±±þµƒ∏þ£¨º¥µ„Pµƒ∫·◊¯±Í£¨‘Ÿ∏˘æðπ¥π…∂®¿Ìø…«Ûµ„Pµƒ◊ð◊¯±Í£¨¥”∂¯«ÛΩ‚£Æ
£®1£©Ω‚Œˆ°ø»ÁÕºÀ˘ æ

£®2£©![]() «∑ÒŒ™°∞÷«ª€»˝Ω«–Œ°±£¨
«∑ÒŒ™°∞÷«ª€»˝Ω«–Œ°±£¨
¿Ì”…»Áœ¬£∫…Ë’˝∑Ω–Œµƒ±þ≥§Œ™![]() £¨
£¨
°þ![]() «
«![]() µƒ÷–µ„£¨°ý
µƒ÷–µ„£¨°ý![]() £¨
£¨
°þ![]() £¨°ý
£¨°ý![]() £¨
£¨![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() «÷±Ω«»˝Ω«–Œ£¨
«÷±Ω«»˝Ω«–Œ£¨
°þ–±±þ![]() …œµƒ÷–œþµ»”⁄
…œµƒ÷–œþµ»”⁄![]() µƒ“ª∞Σ¨
µƒ“ª∞Σ¨
°ý![]() Œ™°∞÷«ª€»˝Ω«–Œ°±£ª
Œ™°∞÷«ª€»˝Ω«–Œ°±£ª
£®3£©»ÁÕºÀ˘ æ£∫

”…°∞÷«ª€»˝Ω«–Œ°±µƒ∂®“Âø…µ√![]() Œ™÷±Ω«»˝Ω«–Œ£¨
Œ™÷±Ω«»˝Ω«–Œ£¨
∏˘æð“‚ø…µ√“ªÃı÷±Ω«±þŒ™1£¨µ±–±±þ◊Ó∂à ±£¨¡Ì“ªÃı÷±Ω«±þ◊Ó∂㨑Ú√ʪ˝»°µ√◊Ó–°÷µ£¨”…¥πœþ∂Œ◊Ó∂Ãø…µ√–±±þ◊Ó∂ÃŒ™3£¨
”…π¥π…∂®¿Ìø…µ√![]() £¨
£¨![]() £¨
£¨
”…π¥π…∂®¿Ìø…«Ûµ√ £¨
£¨
𠵄![]() µƒ◊¯±Í
µƒ◊¯±Í £¨
£¨ £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£¨µ»±þ°˜ABC£¨µ„ E ‘⁄ BA µƒ—”≥§œþ…œ£¨µ„ D ‘⁄ BC …œ£¨«“ ED=EC£Æ
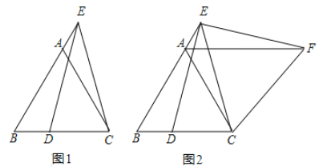
£®1£©»ÁÕº 1£¨«Û÷§£∫AE=DB£ª
£®2£©»ÁÕº 2£¨Ω´°˜BCE »∆µ„ C À≥ ±’Ζ˝◊™ 60°„÷¡°˜ACF£®µ„ B°¢E µƒ∂‘”¶µ„∑÷±Œ™µ„ A°¢F£©£¨¡¨Ω” EF£Æ‘⁄≤ªÃ̺”»Œ∫Œ∏®÷˙œþµƒ«Èøˆœ¬£¨«Î÷±Ω”–¥≥ˆÕº÷–Àƒ∂‘œþ∂Œ£¨ π√ø∂‘œþ∂Œ≥§∂»÷Æ≤Óµ»”⁄ AB µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
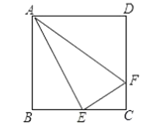
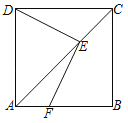
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒABCD÷–£¨AB£Ω3£¨µ„EŒ™∂‘Ω«œþAC…œ“ªµ„£¨EF°ÕDEΩªAB”⁄F£¨»ÙÀƒ±þ–ŒAFEDµƒ√ʪ˝Œ™4£¨‘ÚÀƒ±þ–ŒAFEDµƒ÷Ð≥§Œ™______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
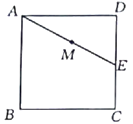
°æƒø°ø»ÁÕº£¨’˝∑Ω–Œ![]() µƒ±þ≥§Œ™
µƒ±þ≥§Œ™![]() £¨µ„
£¨µ„![]() Œ™
Œ™![]() ±þ…œ“ªµ„£¨
±þ…œ“ªµ„£¨![]() £¨µ„
£¨µ„![]() Œ™
Œ™![]() µƒ÷–µ„£¨π˝µ„
µƒ÷–µ„£¨π˝µ„![]() ◊˜÷±œþ∑÷±”Î
◊˜÷±œþ∑÷±”Î![]() £¨
£¨![]() œýΩª”⁄µ„
œýΩª”⁄µ„![]() £¨
£¨![]() .»Ù
.»Ù![]() £¨‘Ú
£¨‘Ú![]() ≥§Œ™______
≥§Œ™______![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
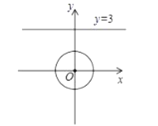
°æƒø°ø»ÁÕº£¨A£¨B «∑¥±»¿˝∫Ø ˝y=![]() ‘⁄µ⁄“ªœÛœÞƒ⁄µƒÕºœÛ…œµƒ¡Ωµ„£¨«“A£¨B¡Ωµ„µƒ∫·◊¯±Í∑÷± «2∫Õ4£¨‘Ú°˜OABµƒ√ʪ˝ «£®°°°°£©
‘⁄µ⁄“ªœÛœÞƒ⁄µƒÕºœÛ…œµƒ¡Ωµ„£¨«“A£¨B¡Ωµ„µƒ∫·◊¯±Í∑÷± «2∫Õ4£¨‘Ú°˜OABµƒ√ʪ˝ «£®°°°°£©
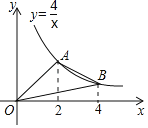
A. 4 B. 3 C. 2 D. 1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ ‘≠–Õ£∫»ÁÕº¢Ÿ£¨‘⁄µ»—¸÷±Ω«»˝Ω«–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() ÷–µ„Œ™
÷–µ„Œ™![]() £¨Ω´œþ∂Œ
£¨Ω´œþ∂Œ![]() »∆µ„
»∆µ„![]() À≥ ±’Ζ˝◊™
À≥ ±’Ζ˝◊™![]() µ√µΩœþ∂Œ
µ√µΩœþ∂Œ![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ±þ…œµƒ∏þ
±þ…œµƒ∏þ![]() £¨“◊÷§
£¨“◊÷§![]() £¨¥”∂¯µ√µΩ
£¨¥”∂¯µ√µΩ![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £Æ
£Æ
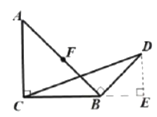
≥ı≤ΩÃΩæø£∫»ÁÕº¢⁄£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() ÷–µ„Œ™
÷–µ„Œ™![]() £ÆΩ´œþ∂Œ
£ÆΩ´œþ∂Œ![]() »∆µ„
»∆µ„![]() À≥ ±’Ζ˝◊™
À≥ ±’Ζ˝◊™![]() µ√µΩœþ∂Œ
µ√µΩœþ∂Œ![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £Æ”√∫¨
£Æ”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ
µƒ¥˙ ˝ Ω±Ì æ![]() µƒ√ʪ˝£¨≤¢Àµ√˜¿Ì”…£Æ
µƒ√ʪ˝£¨≤¢Àµ√˜¿Ì”…£Æ
ºÚµ•”¶”√£∫»ÁÕº¢€£¨‘⁄µ»—¸»˝Ω«–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() ÷–µ„Œ™
÷–µ„Œ™![]() £ÆΩ´œþ∂Œ
£ÆΩ´œþ∂Œ![]() »∆µ„
»∆µ„![]() À≥ ±’Ζ˝◊™
À≥ ±’Ζ˝◊™![]() µ√µΩœþ∂Œ
µ√µΩœþ∂Œ![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨÷±Ω”–¥≥ˆ
£¨÷±Ω”–¥≥ˆ![]() µƒ√ʪ˝£Æ(”√∫¨
µƒ√ʪ˝£Æ(”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ)
µƒ¥˙ ˝ Ω±Ì æ)

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–≈◊ŒÔœþy£Ω£®x+1£©£®x©Å3£©”Îx÷·œýΩª”⁄A°¢B¡Ωµ„£¨»Ù‘⁄≈◊ŒÔœþ…œ”–«“÷ª”–»˝∏ˆ≤ªÕ¨µƒµ„C1°¢C2°¢C3£¨ πµ√°˜ABC1°¢°˜ABC2°¢°˜ABC3µƒ√ʪ˝∂ºµ»”⁄m£¨‘Úmµƒ÷µ «£®°°°°£©
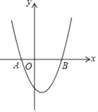
A. 6 B. 8 C. 12 D. 16
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
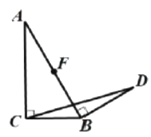
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œACB=90°„£¨CA=8£¨CB=6£¨∂ص„P¥”C≥ˆ∑¢—ÿCA∑ΩœÚ£¨“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚAµ„‘»ÀŸ‘À∂Ø£¨µΩ¥ÔAµ„∫Û¡¢º¥“‘‘≠¿¥ÀŸ∂»—ÿAC∑µªÿ£ªÕ¨ ±∂ص„Q¥”µ„A≥ˆ∑¢—ÿAB“‘√ø√Î1∏ˆµ•Œª≥§∂»œÚµ„B‘»ÀŸ‘À∂Ø£¨µ±QµΩ¥ÔB ±£¨P°¢Q¡Ωµ„Õ¨ ±Õ£÷π‘À∂أƅËP°¢Q‘À∂صƒ ±º‰Œ™t√Σ®t£æ0£©£Æ
£®1£©µ±tŒ™∫Œ÷µ ±£¨PQ°ŒCB£ø
£®2£©‘⁄µ„P¥”CœÚA‘À∂صƒπ˝≥Ã÷–£¨‘⁄CB…œ «∑ҥʑ⁄µ„E π°˜CEP”ΰ˜PQA»´µ»£ø»Ù¥Ê‘⁄£¨«Û≥ˆCEµƒ≥§£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©∞ÈÀÊ◊≈P°¢Q¡Ωµ„µƒ‘À∂Ø£¨œþ∂ŒPQµƒ¥π÷±∆Ω∑÷œþDFΩªPQ”⁄µ„D£¨Ωª’€œþQB©ÅBC©ÅCP”⁄µ„F£Æµ±DFæ≠π˝µ„C ±£¨«Û≥ˆtµƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒABCD±þ≥§Œ™2£¨E «ABµƒ÷–µ„£¨“‘EŒ™‘≤–ƒ£¨œþ∂ŒEDµƒ≥§Œ™∞Îæ∂◊˜∞Α≤£¨Ωª÷±œþAB”⁄µ„M£¨N£¨∑÷±“‘œþ∂ŒMD£¨NDŒ™÷±æ∂◊˜∞Α≤£¨‘ÚÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝Œ™_____________

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com