
【题目】为了开展阳光体育运动,坚持让中小学生“每天锻炼一小时”,体育局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了340名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).
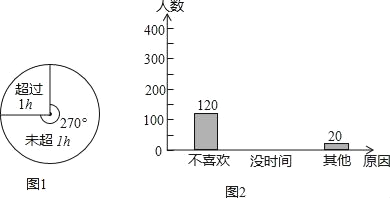
根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2015年全市中小学生约18万人,按此调查,可以估计2015年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2017年全市中小学生每天锻炼未超过1h的人数减少到8.64万人,求2015年至2017年锻炼未超过1h人数的年平均降低的百分率.
【答案】(1)115人;(2)超过1h的约有4.5万人;(3)20%.
【解析】
(1)由于随机调查了340名学生,首先根据扇形统计图可知锻炼未超过1h的中小学生占=75%,从而得出锻炼未超过1h的中小学生人数;又根据题意,将锻炼未超过1h的原因所得的数据制成了频数分布直方图,由频数分布直方图得到不喜欢的人数和其他的人数分别是120和20,由此即可求出“没时间”的人数,然后就可以补全频数分布直方图;
(2)根据扇形统计图可以知道每天锻炼超过1h的百分比,然后乘以18万即可得到2015年全市中小学生每天锻炼超过1h的约有多少人;
(3)设2015年至2017年锻炼未超过1h人数的年平均降低的百分率为x,可以列出方程18×0.75(1﹣x)2=8.64,解方程即可求出2015年至2017年锻炼未超过1h人数的年平均降低的百分率.
解:(1)∵随机调查了340名学生,
∴锻炼未超过1h的中小学生有340×![]() =255人,
=255人,
又∵不喜欢的人数和其他的人数分别是120和20,
∴“没时间”的人数为255﹣120﹣20=115人,
频数分布直方图如图所示:
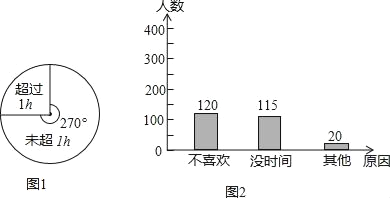
(2)根据扇形统计图知道:
每天锻炼超过1h的百分比为18×![]() =4.5万人.
=4.5万人.
故估计2015年全市中小学生每天锻炼超过1h的约有4.5万人;
(3)设2015年至2017年锻炼未超过1h人数的年平均降低的百分率为x.
由题意得:18×0.75(1﹣x)2=8.64,
解得x=0.2,x=1.8(舍去).
答:2015年至2017年锻炼未超过1h人数的年平均降低的百分率为20%.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】为了了解初一年级学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:

(I)本次随机抽样调查的学生人数为 ,图①中的m的值为 ;
(II)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(III)若该区初一年级共有学生2500人,请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
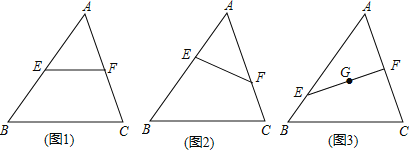
【题目】在△ABC中,E、F分别为线段AB、AC上的点(不与A、B、C重合).
(1)如图1,若EF∥BC,求证:![]()
(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若EF上一点G恰为△ABC的重心,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
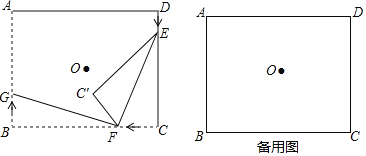
【题目】如图,点O为矩形ABCD对角线交点,![]() ,
,![]() ,点E、F、G分别从D,C,B三点同时出发,沿矩形的边DC、CB、BA匀速运动,点E的运动速度为
,点E、F、G分别从D,C,B三点同时出发,沿矩形的边DC、CB、BA匀速运动,点E的运动速度为![]() ,点F的运动速度为
,点F的运动速度为![]() ,点G的运动速度为
,点G的运动速度为![]() ,当点F到达点
,当点F到达点![]() 点F与点B重合
点F与点B重合![]() 时,三个点随之停止运动
时,三个点随之停止运动![]() 在运动过程中,
在运动过程中,![]() 关于直线EF的对称图形是
关于直线EF的对称图形是![]() 设点E、F、G运动的时间为
设点E、F、G运动的时间为![]() 单位:
单位:![]()
![]() 当
当![]() ______s时,四边形
______s时,四边形![]() 为正方形;
为正方形;
![]() 若以点E、C、F为顶点的三角形与以点F、B、G为顶点的三角形相似,求t的值;
若以点E、C、F为顶点的三角形与以点F、B、G为顶点的三角形相似,求t的值;
![]() 是否存在实数t,使得点
是否存在实数t,使得点![]() 与点O重合?若存在,直接写出t的值;若不存在,请说明理由.
与点O重合?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
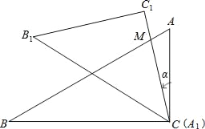
【题目】如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠B1A1 C1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.
(1)计算A1C1的长;
(2)当α=30°时,证明:B1C1∥AB;
(3)若a=![]() ,当α=45°时,计算两个三角板重叠部分图形的面积;
,当α=45°时,计算两个三角板重叠部分图形的面积;
(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.
(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=2﹣
,tan15°=2﹣![]() ,sin75°=
,sin75°=![]() ,cos75°=
,cos75°=![]() ,tan75°=2+
,tan75°=2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
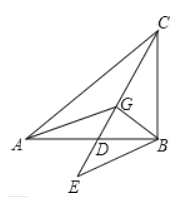
【题目】如图,点G是△ABC的重心,CG的延长线交AB于D,GA=5,GC=4,GB=3,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且c>b>a,若Rt△ABC是奇异三角形,求a:b:c;
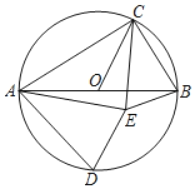
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆![]() 中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形:
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com