
分析 (1)y=2x+4与x轴交于点A,与y轴交于点B,与直线y=8-2x交于点C,根据坐标轴上点的坐标特征可确定A、B、C的坐标;
(2)若直线l1经过原点且将△AOB分成面积相等的两部分,直线l1恰好经过AB的中点,求得AB的中点坐标,利用待定系数法求得函数解析式即可;
(3)设D点坐标为(x,2x+4),利用三角形的面积求法和S△AMD=$\frac{1}{3}$S△AOC,建立方程求得点D坐标,进一步利用待定系数法求得函数解析式即可.
解答 解:(1)如图,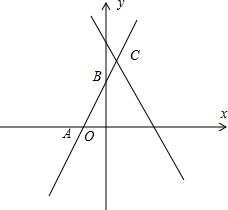
直线y=2x+4与x轴交于点A,
当x=0时,y=4,则B(0,4),
当y=0时,2x+4=0,解得x=-2,则A(-2,0),
解方程组$\left\{\begin{array}{l}{y=2x+4}\\{y=8-2x}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$,则C(2,6);
(2)如图,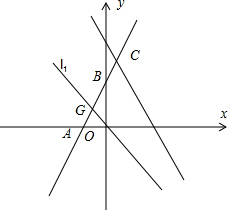
∵直线l1经过原点且将△AOB分成面积相等的两部分,
∴OG是△AOB的中线,
∴G点坐标为($\frac{-2+0}{2}$,$\frac{0+4}{2}$),即(-1,2),
设l1=kx,
代入点G得k=-2,
∴这条直线l1的函数表达式为l1=-2x.
(3)如图,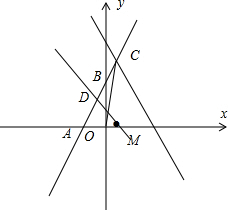
设D点坐标为(x,2x+4),
∵S△AMD=$\frac{1}{3}$S△AOC,
∴$\frac{1}{2}$×3×(2x+4)=$\frac{1}{2}$×2×6
解得:x=0,
D点坐标为(0,4),
设l2=kx+b,
代入点(0,4)和点M(1,0)得出l2=-4x+4.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了三角形面积公式.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲的射击成绩更稳定 | B. | 乙的射击成绩更稳定 | ||
| C. | 甲、乙的射击成绩一样稳定 | D. | 无法确定甲、乙射击成绩谁更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届山东省滨州市邹平双语学校一二区九年级上学期期中考试数学试卷 题型:填空题
在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连接PA,PB.若PB=4,则PA的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com