
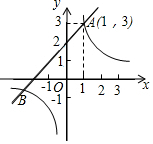 如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).
如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).分析 (1)一次函数和反比例函数都是一个未知字母,把交点代入函数解析式即可;
(2)应从交点处看在交点的哪一边一次函数的函数值>反比例函数的函数值.
解答 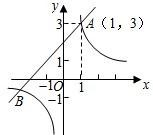 解:(1)由题意,得3=1+m,
解:(1)由题意,得3=1+m,
解得:m=2.
所以一次函数的解析式为y1=x+2.
由题意,得3=$\frac{k}{1}$,
解得:k=3.
所以反比例函数的解析式为y2=$\frac{3}{x}$.
由题意,得x+2=$\frac{3}{x}$,
解得x1=1,x2=-3.
当x2=-3时,y1=y2=-1,
所以交点B(-3,-1).
(2)由图象可知,当-3≤x<0或x≥1时,函数值y1≥y2.
点评 本题考查用待定系数法求函数解析式;需注意:无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考.


科目:初中数学 来源: 题型:解答题
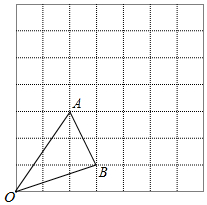 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知Rt△ABC是直角边长为l的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…依此类推.
如图,已知Rt△ABC是直角边长为l的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…依此类推.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com