
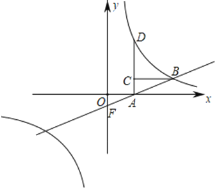
【题目】 如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴相交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求反比例函数和一次函数的表达式;
(2)直接写出反比例函数值大于一次函数值时自变量的取值范围.
【答案】(1)![]() ,
,![]() ;(2)0<x<9或x<-6
;(2)0<x<9或x<-6
【解析】
(1)由点C的坐标为(3,2)得AC=2,而AC:AD=1:3,得到AD=6,则D点坐标为(3,6),然后利用待定系数法确定双曲线的解析式,把y=2代入求得B的坐标,然后根据待定系数法即可求得直线AB的解析式;
(2)联立解析式,解方程组求得另一个交点坐标,然后利用图象即可求出答案.
(1)∵点C的坐标为(3,2),
∴OA=3,AC=2,
∵AC:AD=1:3,
∴AD=6,
∴点D的坐标为(3,6),
设双曲线的解析式为![]() ,
,
∴k=3×6=18,
∴双曲线的解析式为:![]() ;
;
设直线AB的解析式为![]() ,
,
∵CB平行于x轴交曲线于点B,
∴B点的纵坐标为2,
代入![]() 得x=9,
得x=9,
∴B点的坐标为(9,2),
把A(3,0)和B(9,2)代入![]() 得
得![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为:![]() ;
;
(2)联立解析式得 ,
,
解得![]() 或
或![]() ,
,
∴反比例函数与一次函数的另一个交点为(-6,-3),
∴根据图象,当x<-6或0<x<9时,反比例函数的图象在一次函数的上方,
∴反比例函数值大于一次函数值时自变量的取值范围是:x<-6或0<x<9.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
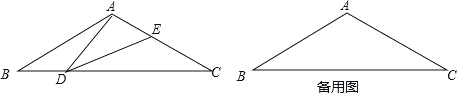
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
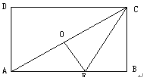
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣1,0),B(m,0),与y轴交于点C(0,﹣2),且∠ACB=90度.
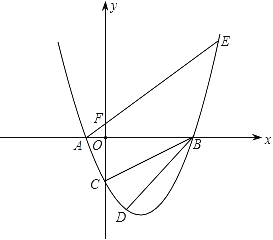
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E,求点D和点E的坐标;
(3)在x轴上是否存在点P,使以点P,B,D为顶点的三角形与三角形AEB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
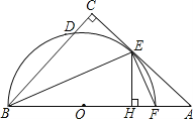
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EF=![]() ,求AF长.
,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
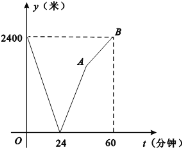
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了______分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
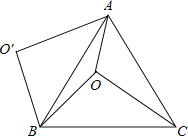
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场按定价销售某种商品时,每件可获利100元;按定价的八折销售该商品5件与将定价降低50元销售该商品6件所获利润相等.
(1)该商品进价、定价分别是多少?
(2)该商场用10000元的总金额购进该商品,并在五一节期间以定价的七折优惠全部售出,在每售出一件该商品时,均捐献![]() 元给社会福利事业,该商场为能获得不低于3000元的利润,求
元给社会福利事业,该商场为能获得不低于3000元的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com