
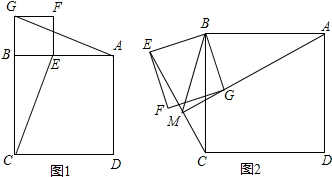
 ��ͼ1��������y=ax2+bx+6��a��0����x�ύ�ڵ�A��2��0���͵�B��-6��0������y�ύ�ڵ�C��
��ͼ1��������y=ax2+bx+6��a��0����x�ύ�ڵ�A��2��0���͵�B��-6��0������y�ύ�ڵ�C������ ��1����A��2��0����B��-6��0������y=ax2+bx+6�ⷽ���鼴�ɣ�
��2����ͼ1�У����������ٵ�P1C=CMʱ����MP2=MCʱ����MP3=MCʱ���ֱ���⼴�ɣ�
��3����ͼ2�У�����BC���Գ�����Q����ʱQA+QC��С�����ֱ��BC�Ľ���ʽ�����������Q���꣮
��4����ͼ3�У���E��m��-$\frac{1}{2}$m2-2m+6��������EO������S�ı���BOCE=S��BOE+S��COE�������κ��������ö��κ��������ʽ�����⣮
��� �⣺��1����A��2��0����B��-6��0������y=ax2+bx+6��$\left\{\begin{array}{l}{4a+2b+6=0}\\{35a-6b+6=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-2}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2-2x+6��
��2����ͼ1�У�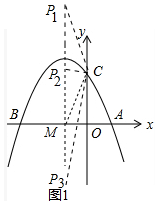
������C��0��6����M��-2��0����
��CM=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$��
�ٵ�P1C=CMʱ���ɵ�P1��-2��12����
�ڵ�MP2=MCʱ��P2��-2��2$\sqrt{10}$����
�۵�MP3=MCʱ��P3��-2��-2$\sqrt{10}$����
�����������������ĵ�P���꣨-2��12����-2��2$\sqrt{10}$����-2��-2$\sqrt{10}$����
��3����ͼ2�У�����BC���Գ�����Q����ʱQA+QC��С��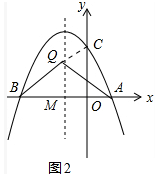
��B��-6��0����C��0��6����
��ֱ��BC�Ľ���ʽΪy=x+6��
���Q��-2��4����
��4����ͼ3�У���E��m��-$\frac{1}{2}$m2-2m+6��������EO��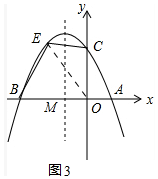
��S�ı���BOCE=S��BOE+S��COE=$\frac{1}{2}$��6����-$\frac{1}{2}$m2-2m+6��+$\frac{1}{2}$��6����-m��=-$\frac{3}{2}$��m+3��2+$\frac{63}{2}$��
��a=-$\frac{3}{2}$��0��
��m=-3ʱ���ı���BOCE�����������ֵΪ$\frac{63}{2}$����ʱ��E��-3��$\frac{15}{2}$����
���� ���⿼����κ����ۺ��⡢����ϵ���������������ε��ж������ʡ���ֵ�����֪ʶ������Ĺؼ���ѧ�����öԳ�ȷ��������⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
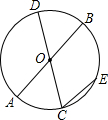 ��ͼ��AB��CD�ǡ�O��ֱ������CE��AB����$\widehat{CE}$�Ķ���Ϊ50�㣬���AOC�Ķ�����
��ͼ��AB��CD�ǡ�O��ֱ������CE��AB����$\widehat{CE}$�Ķ���Ϊ50�㣬���AOC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | AB=A��B�䣬BC=B��C�䣬��A=��A�� | B�� | ��A=��A�䣬��B=��B�䣬AC=B��C�� | ||
| C�� | ��A=��A�䣬��B=��B�䣬��C=��C�� | D�� | AB=A��B�䣬BC=B��C�䣬AC=A��C�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ε��ĸ��Ƕ���ֱ�� | B�� | �����εĶԽ����ഹֱ | ||
| C�� | �ڱ���ȵľ����������� | D�� | �Խ�����ȵ�ƽ���ı��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com