
【题目】实践与探究
宽与长的比是![]() (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
下面我们通过折纸得到黄金矩形。
第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。

第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是![]() 。
。
第三步,折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处,折痕为
处,折痕为![]() 。
。
第四步,展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ;过点
;过点![]() 折出折痕
折出折痕![]() ,使
,使![]() 。
。

(1)上述第三步将![]() 折到
折到![]() 处后,得到一个四边形
处后,得到一个四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由。
的形状,并说明理由。
(2)上述第四步折出折痕![]() 后得到一个四边形
后得到一个四边形![]() ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设![]() 的长度为2)
的长度为2)
(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形![]() 除外,直接写出答案,不需证明,可能参考数值:
除外,直接写出答案,不需证明,可能参考数值:![]() )
)
(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________.
【答案】(1)四边形![]() 是菱形,见解析;(2)见解析;(3)黄金矩形
是菱形,见解析;(2)见解析;(3)黄金矩形![]() (或黄金矩形
(或黄金矩形![]() );(4)希腊的巴特农神庙(或巴黎圣母院).
);(4)希腊的巴特农神庙(或巴黎圣母院).
【解析】
(1)根据菱形的判定即可求解;
(2)根据菱形的性质及折叠得到![]() ,即可证明;
,即可证明;
(3)
(1)解:
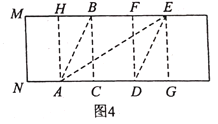
四边形![]() 是菱形,
是菱形,
理由如下:
由矩形纸片可得![]() ,
,
∴![]() ,
,
由折叠可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
又由折叠可得![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
(2)证明:设![]() 的长度为2,
的长度为2,
由正方形![]() 可得,
可得,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]() ,由折叠可得,
,由折叠可得,![]() ,
,
在![]() 中,根据勾股定理,
中,根据勾股定理,![]() ,
,
由折叠可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴矩形![]() 是黄金矩形;
是黄金矩形;
(3)黄金矩形![]()
理由:AG=AD+DG=AB+DG=![]()
AH=2,
∴![]()
∴四边形AGEH为黄金矩形
(4)希腊的巴特农神庙(或巴黎圣母院)


科目:初中数学 来源: 题型:
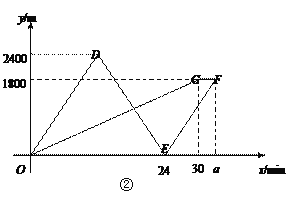
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;
②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2cm,AC=5cm,SABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
(1)在运动过程中,四边形AECF的形状是____;
(2)t=____时,四边形AECF是矩形;
(3)求当t等于多少时,四边形AECF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正确的个数为( )
;其中正确的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
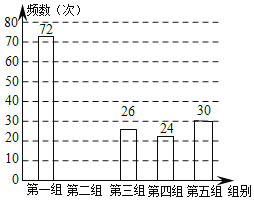
组别 | 单次营运里程“x”(千米) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据以上信息,解答下列问题:
(1)表中a= ,样本中“单次营运里程”不超过15千米的频率为 ;
(2)请把频数分布直方图补充完整;
(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;

(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
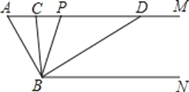
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣2)﹣1﹣|﹣![]() |+(
|+(![]() ﹣1)0+cos45°.
﹣1)0+cos45°.
(2)已知m2﹣5m﹣14=0,求(m﹣1)(2m﹣1)﹣(m+1)2+1的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com