
【题目】已知:在△ABC中,∠ACB=90°,CD⊥AB于D,BE:AB=3:5,若CE= ![]() ,cos∠ACD=
,cos∠ACD= ![]() ,求tan∠AEC的值及CD的长.
,求tan∠AEC的值及CD的长.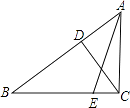
【答案】解:在Rt△ACD与Rt△ABC中,
∵∠ABC+∠CAD=90°,∠ACD+∠CAD=90°,∴∠ABC=∠ACD,
∴ ![]()
在Rt△ABC中, ![]()
令BC=4k,AB=5k,则AC=3k
由BE:AB=3:5,知BE=3k
则 ![]() ,则
,则 ![]() ,
, ![]() .
.
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() .
.
【解析】在Rt△ACD与Rt△ABC中,∠ABC+∠CAD=90°,∠ACD+∠CAD=90°,∴∠ABC=∠ACD,得到 cos∠ABC = cos∠ACD = ![]() ,在Rt△ABC中,
,在Rt△ABC中,![]() =
=![]() ,
,
令BC=4k,AB=5k,则AC=3k,由BE:AB=3:5,知BE=3k,在Rt △ACD中 ,cos∠ACD=![]() ,所以CD=
,所以CD=![]() .
.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半.这样的图形有( )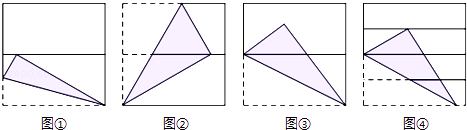
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,若两车之间的距离S关于客车行驶时间X的函数关系式当0≤x≤![]() 时,S=-160x+600;当
时,S=-160x+600;当![]() ≤x≤6时,S=160x﹣600;当6≤x≤10时,S=60x,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象可能是( )
≤x≤6时,S=160x﹣600;当6≤x≤10时,S=60x,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),y1,y2与x的函数关系图象可能是( )
A. 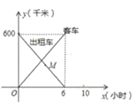 B.
B. 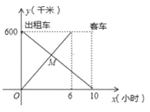
C. 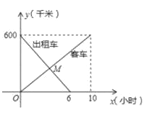 D.
D. 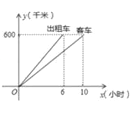
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 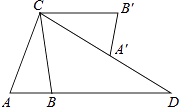
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正整数m,若m=pq(p≥q>0,且p,q为整数),当p-q最小时,则称pq为m的“最佳分解”,并规定f(m)=![]() (如:12的分解有12×1,6×2,4×3,其中,4×3为12的最佳分解,则f(12)=
(如:12的分解有12×1,6×2,4×3,其中,4×3为12的最佳分解,则f(12)=![]() ).关于f(m)有下列判断:①f(27)=3;②f(13)=
).关于f(m)有下列判断:①f(27)=3;②f(13)=![]() ;③f(2018)=
;③f(2018)=![]() ;④f(2)=f(32).其中,正确判断的序号是______.
;④f(2)=f(32).其中,正确判断的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解.例如:![]() ,
,![]() 都是因式分解.因式分解也可称为分解因式.
都是因式分解.因式分解也可称为分解因式.
材料2:只含有一个未知数,且未知数的最高次数是![]() 的整式方程称作一元二次方程.一元二次方程的般形式是:
的整式方程称作一元二次方程.一元二次方程的般形式是:![]() (其中
(其中![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() ).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
例如解方程;![]()
![]()
![]()
![]() 或
或![]()
![]() 原方程的解是
原方程的解是![]() ,
,![]()
∴原方程的解是![]() ,
,![]()
又如解方程:![]()
![]()
![]()
![]()
![]() 原方程的解是
原方程的解是![]()
请阅读以上材料回答以下问题:
(1)若![]() ,则
,则![]() _______;
_______;![]() _______;
_______;
(2)请将下列多项式因式分解:
![]() _______,
_______,![]() ________;
________;
(3)在平面直角坐标系中,已知点![]() ,
,![]() ,其中
,其中![]() 是一元二次方程
是一元二次方程![]() 的解,
的解,![]() 为任意实数,求
为任意实数,求![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
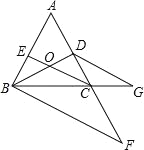
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
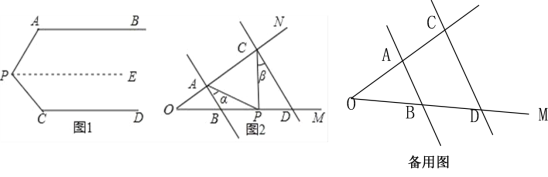
【题目】问题情境:如图1,AB∥CD,∠PAB=125°,∠PCD=135°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 度。
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,①如果点P运动到D点右侧(不包括D点),则∠APC与α、β之间的数量关系为 .②如果点P运动到B点左侧(不包括B点),则∠APC与α、β之间的数量关系 .(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com