
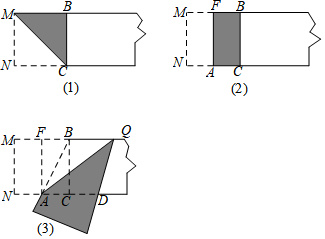
·ÖĪö £Ø1£©ĻČÖ¤Ć÷ĖıߊĪMNCBĪŖÕż·½ŠĪ£¬ŌŁĄūÓĆÕŪµžµĆ£ŗCA=1£¬AB=AD£¬ĖłŅŌCD=AD-AC£¬æÉµĆ½įĀŪ£»
£Ø2£©øł¾ŻĘ½ŠŠĻߵĊŌÖŹµĆÕŪµžµĆ£ŗ”ĻBAQ=”ĻBQA£¬ÓÉµČ½Ē¶ŌµČ±ßµĆ£ŗAB=BQ£¬ÓÉŅ»×é¶Ō±ßĘ½ŠŠĒŅĻąµČæÉµĆ£ŗĖıߊĪABQDŹĒĘ½ŠŠĖıߊĪ£¬ŌŁÓÉAB=AD£¬æɵĆĖıߊĪABQDŹĒĮāŠĪ£®
½ā“š ½ā£ŗ£Ø1£©”ß”ĻM=”ĻN=”ĻMBC=90”ć£¬
”ąĖıߊĪMNCBŹĒ¾ŲŠĪ£¬
”ßMB=MN=2£¬
”ą¾ŲŠĪMNCBŹĒÕż·½ŠĪ£¬
”ąNC=CB=2£¬
ÓÉÕŪµžµĆ£ŗAN=AC=$\frac{1}{2}$NC=1£¬
Rt”÷ACBÖŠ£¬Óɹ“¹É¶ØĄķµĆ£ŗAB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$£¬
”ąAD=AB=$\sqrt{5}$£¬
”ąCD=AD-AC=$\sqrt{5}$-1£»
£Ø2£©ĖıߊĪABQDŹĒĮāŠĪ£¬ĄķÓÉŹĒ£ŗ
ÓÉÕŪµžµĆ£ŗAB=AD£¬”ĻBAQ=”ĻQAD£¬
”ßBQ”ĪAD£¬
”ą”ĻBQA=”ĻQAD£¬
”ą”ĻBAQ=”ĻBQA£¬
”ąAB=BQ£¬
”ąBQ=AD£¬BQ”ĪAD£¬
”ąĖıߊĪABQDŹĒĘ½ŠŠĖıߊĪ£¬
”ßAB=AD£¬
”ąĖıߊĪABQDŹĒĮāŠĪ£®
µćĘĄ ±¾ĢāŹĒĖıߊĪµÄ×ŪŗĻĢā£¬ÄѶȏŹÖŠ£¬æ¼²éĮĖĮāŠĪ”¢Õż·½ŠĪ”¢Ę½ŠŠĖıߊĪ”¢¾ŲŠĪµÄÅŠ¶ØŗĶŠŌÖŹŅŌ¼°ÕŪµžµÄŠŌÖŹ£¬²¢ĄūÓĆŹżŠĪ½įŗĻµÄĖ¼Ļė½ā¾öĪŹĢā£®


 Õć“óÓÅѧŠ”ѧğ¼¶ĻĪ½Ó½Ż¾¶Õć½“óѧ³ö°ęÉēĻµĮŠ“š°ø
Õć“óÓÅѧŠ”ѧğ¼¶ĻĪ½Ó½Ż¾¶Õć½“óѧ³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ¾ŲŠĪ | B£® | ĮāŠĪ | C£® | Õż·½ŠĪ | D£® | ĪŽ·ØČ·¶Ø |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
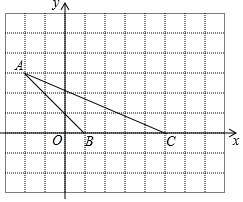 ČēĶ¼ĖłŹ¾£¬Š”·½øń±ß³¤ĪŖ1øöµ„Ī»£¬
ČēĶ¼ĖłŹ¾£¬Š”·½øń±ß³¤ĪŖ1øöµ„Ī»£¬²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ŗÆŹżĶ¼Ļó¾¹żµć£Ø-2£¬1£© | B£® | yĖęxµÄŌö“ó¶ų¼õŠ” | ||
| C£® | ŗÆŹżĶ¼Ļó¾¹żµŚŅ»”¢ČżĻóĻŽ | D£® | ²»ĀŪxČ”ŗĪÖµ£¬×ÜÓŠy£¼0 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ĮĖ½ā±¾ŹŠÖŠŃ§ÉśĆæĢģѧĻ°ĖłÓƵď±¼ä£¬²ÉÓĆČ«Ćęµ÷²éµÄ·½Ź½ | |
| B£® | ĪŖ±£Ö¤ŌĖŌŲ»š¼żµÄ³É¹¦·¢É䣬¶ŌĘäĖłÓŠµÄĮć²æ¼ž²ÉÓĆ³éŃłµ÷²éµÄ·½Ź½ | |
| C£® | ĮĖ½āijŹŠĆæĢģµÄĮ÷¶ÆČĖæŚŹż£¬²ÉÓĆČ«Ćęµ÷²éµÄ·½Ź½ | |
| D£® | ĮĖ½āČ«ŹŠÖŠŃ§ÉśµÄŹÓĮ¦Ēéæö£¬²ÉÓĆ³éŃłµ÷²éµÄ·½Ź½ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
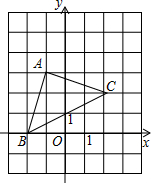 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬A£¬BĮ½µćµÄ×ų±ź·Ö±šĪŖA£Ø-1£¬3£©£¬B£Ø-2£¬0£©£¬C£Ø2£¬2£©£¬Ōņ”÷ABCµÄĆ껿ŹĒ5£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬A£¬BĮ½µćµÄ×ų±ź·Ö±šĪŖA£Ø-1£¬3£©£¬B£Ø-2£¬0£©£¬C£Ø2£¬2£©£¬Ōņ”÷ABCµÄĆ껿ŹĒ5£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
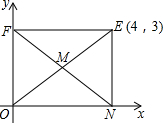 ”¾ŌĶĮ”æ
”¾ŌĶĮ”æ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 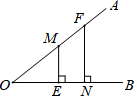 | B£® |  | C£® | 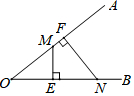 | D£® |  |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com