
【题目】如图,在△ABC中,∠ACB=90°, ∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒2个单位的速度运动,当点P到达点B时,P、Q同时停止运动,连结PQ、QA.设点P运动的时间为t秒.
(1)当CQ=2BP时,求t的值;
(2)当t为何值时QP=QA;
(3)若线段PQ的中垂线与线段BC相交(包括线段的端点),则t的取值范围是 .(直接写出答案)
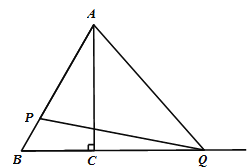
【答案】(1)4;(2)4.5;(3)1.5≤t≤3
【解析】试题分析:(1)根据直角三角形的性质求出AB,根据题意列出方程,解方程即可;
(2)根据相似三角形的性质求出PE、BE,根据勾股定理列方程,解方程求出t;
(3)根据线段垂直平分线的性质、勾股定理列式计算.
试题解析:解:(1)∵∠ACB=90°,∠ABC=60°,∴∠BAC=30°,∴AB=2BC=12,AC=![]() ,由题意得,CQ=2t,BP=12﹣2t,则2t=2(12﹣2t),得t=4;
,由题意得,CQ=2t,BP=12﹣2t,则2t=2(12﹣2t),得t=4;
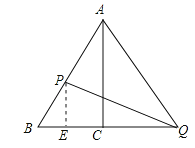
(2)作PE⊥BQ于E,则PE∥AC,∴△BPE∽△BAC,∴ ![]() ,解得,PE=
,解得,PE= ![]() ,BE=6﹣t,则EQ=EC+CQ=3t,∴PQ2=3(6﹣t)2+9t2,∵∠ACQ=90°,∴AQ2=AC2+CQ2=108+4t2,由题意得,108+4t2=3(6﹣t)2+9t2,解得,t=4.5;
,BE=6﹣t,则EQ=EC+CQ=3t,∴PQ2=3(6﹣t)2+9t2,∵∠ACQ=90°,∴AQ2=AC2+CQ2=108+4t2,由题意得,108+4t2=3(6﹣t)2+9t2,解得,t=4.5;
(3)当BP=BQ时,12﹣2t=6+2t,解得,t=1.5,当CP=CQ时,3(6﹣t)2+t2=(2t)2,解得,t=3,则当1.5≤t≤3时,线段PQ的中垂线与线段BC相交,故答案为:1.5≤t≤3.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
(1)当t=2时,求S的值;
(2)若S<5时,求t的取值范围.
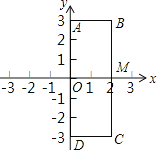
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店有单价为10元、15元和20元的三种文具盒出售,该商店统计了2014年3月份这三种文具盒的销售情况,并绘制统计图(不完整)如下: 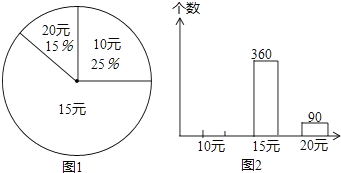
(1)这次调查中一共抽取了多少个文具盒?
(2)求出图1中表示“15元”的扇形所占圆心角的度数;
(3)在图2中把条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() ﹣2kx+
﹣2kx+![]() +2=2(1﹣x)有两个实数根
+2=2(1﹣x)有两个实数根![]() ,
,![]() ,
,
(1)求实数k的取值范围;
(2)若方程的两实根![]() ,
,![]() 满足|
满足|![]() |=
|=![]() ﹣1,求k的值.
﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com