
如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.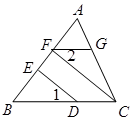
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
解析试题分析:根据垂直的定义及平行线的判定和性质依次分析即可.
∵CF⊥AB ,DE⊥AB (已知)
∴∠BED=90° ,∠BFC=90°( 垂直定义 )
∴∠BED=∠BFC ( 等量代换 )
∴ED∥FC ( 同位角相等,两直线平行 )
∴∠1=∠BCF ( 两直线平行,同位角相等 )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( 等量代换 )
∴FG∥BC ( 内错角相等,两直线平行 )
考点:垂直的定义,平行线的判定和性质
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com