
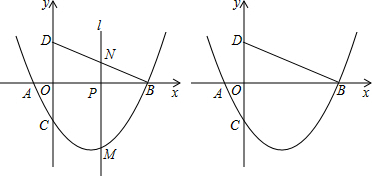
���� ��1�����������߽���ʽ�������A��B��C�����ꣻ
��2���ٿ����ֱ��BD�Ľ���ʽ������m�ɱ�ʾ��MN�ij���������ö��κ������������MN�����ֵ�����ж�MN��CD�Ƿ���ȼ��ɣ����������֪��BM��BD��DM��BD����BM��BDʱ�����M������꣬�Ӷ��ɱ�ʾ��BP��MP�ij������á�OBD�ס�PMB���ɵõ�����M������ķ��̣��Ӷ������M������ꣻ��DM��BDʱ����������֪A��������������A��D��������ֱ��AD����ʽ������ֱ��AD�������߽���ʽ������������������M������꣮
��� �⣺
��1����y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�У���y=0�ɵ�0=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�����x=-1��x=4��
��A��-1��0����B��4��0����
��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2�У���x=0�ɵ�y=-2��
��C��0��-2����
��2���١�D��C����x��Գƣ�
��D��0��2������B��4��0����
�����ֱ��BD����ʽΪy=kx+2����B���������ɵ�4k+2=0�����k=-$\frac{1}{2}$��
��ֱ��BD����ʽΪy=-$\frac{1}{2}$x+2��
��P��m��0����
��N��m��-$\frac{1}{2}$m+2����M��m��$\frac{1}{2}$m2-$\frac{3}{2}$m-2����
��P���߶�OB�ϣ�
��M��x���·���
��MN=-$\frac{1}{2}$m+2-��$\frac{1}{2}$m2-$\frac{3}{2}$m-2��=-$\frac{1}{2}$m2+m+4=-$\frac{1}{2}$��m-1��2+$\frac{9}{2}$��
��-$\frac{1}{2}$��0��
�൱m=1ʱ��MN�����ֵ�����ֵΪ$\frac{9}{2}$��
��CD=4��MN��
���ı���DCMN����ƽ���ı��Σ�
�ڵ���BDM����BDΪֱ�DZߵ�ֱ��������ʱ��ֻ��MB��BD��DM��BD��
��MB��BDʱ����ͼ1��
��P��m��0������M��m��$\frac{1}{2}$m2-$\frac{3}{2}$m-2������B��4��0����D��0��2����
��BP=|4-m|��PM=|$\frac{1}{2}$m2-$\frac{3}{2}$m-2|��OB=4��OD=2��
�ߡ�MBD=90�㣬
���OBD+��PBM=��ODB+��OBD=90�㣬
���ODB=��PMB��
���OBD�ס�PMB��
��$\frac{OB}{MP}$=$\frac{OD}{PB}$����$\frac{4}{|\frac{1}{2}{m}^{2}-\frac{3}{2}m-2|}$=$\frac{2}{|m-4|}$�����m=3��m=4����ȥ����
��M��������3��-2����
��MD��BDʱ����ͼ2��
��OA=1��OD=2��OB=4��
��$\frac{OA}{OD}$=$\frac{OD}{OB}$���ҡ�AOD=��BOD��
���AOD�ס�DOB��
���ADO=��DBO��
���ADB=��ADO+��BDO=��DBO+��BDO=90�㣬��AD��BD��
��A�㼴Ϊ����������M�㣬��ʱM����Ϊ��-1��0����
��D��0��2����
�����ֱ��AD����ʽΪy=kx+2��
��A���������ɵ�0=-k+2�����k=2��
��ֱ��AD����ʽΪy=2x+2��
����ֱ��AD�������߽���ʽ�ɵ�$\left\{\begin{array}{l}{y=2x+2}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=18}\end{array}\right.$��
��ֱ��AD�ϵ���һM������Ϊ��8��18����
���Ͽ�֪�������������ĵ�M��������Ϊ��3��-2����-1��0����8��18����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ͼ����������Ľ��㡢����ϵ���������κ��������ʡ����������ε��ж������ʡ�����˼���֪ʶ���ڣ�1����ע�⺯��ͼ���������ύ������ڣ�2������m��ʾ��MN�ij��ǽ���Ĺؼ����ڣ�3����ȷ����M��λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 cm | B�� | 5$\sqrt{3}$cm | C�� | $\frac{5}{2}$$\sqrt{3}$ cm | D�� | 5 cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
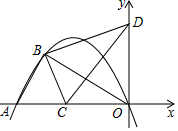 ��ͼ��������y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$��x�ύ�ڵ�A��ԭ��O����B��-8��n�����������ϣ�����AB��OB��
��ͼ��������y=$-\frac{1}{4}{x}^{2}-\frac{5}{2}x$��x�ύ�ڵ�A��ԭ��O����B��-8��n�����������ϣ�����AB��OB���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com