
【题目】如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
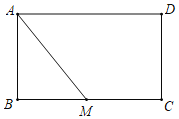
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
【答案】(1)过D 作DE⊥AM于E,△ADE即为所求;见解析;(2)AE=![]() .
.
【解析】
(1)根据题意作出图形即可;
(2)先根据矩形的性质,得到AD∥BC,则∠DAE=∠AMB,又由∠DEA=∠B,根据有两角对应相等的两三角形相似,即可证明出△DAE∽△AMB,根据相似三角形的对应边成比例,即可求出DE的长,根据勾股定理即可得到结论.
解:(1)过D 作DE⊥AM于E,△ADE即为所求;
(2)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AMB,
又∵∠DEA=∠B=90°,
∴△DAE∽△AMB,
∴DE:AD=AB:AM,
∵M是边BC的中点,BC=6,
∴BM=3,
又∵AB=4,∠B=90°,
∴AM=5,
∴DE:6=4:5,
∴DE=![]() ,
,
∴AE=![]() =
=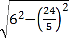 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司生产的一种商品其售价是成本的1.5倍,当售价降低5元时商品的利润率为25%.若不进行任何推广年销售量为1万件.为了获得更好的利益,公司准备拿出一定的资金做推广,根据经验,每年投入的推广费x万元时销售量y(万件)是x的二次函数:当x为1万元时,y是1.5(万件).当x为2万元时,y是1.8(万件).
(1)求该商品每件的的成本与售价分别是多少元?
(2)求出年利润与年推广费x的函数关系式;
(3)如果投入的年推广告费为1万到3万元(包括1万和3万元),问推广费在什么范同内,公司获得的年利润随推广费的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
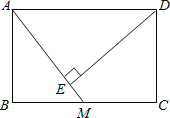
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
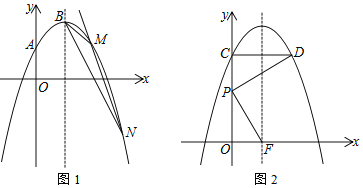
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南边防部队在戍边卫国的艰辛历程中,为祖国和人民建立了不可磨灭的功勋.为保障边防部队的生活,现从甲、乙两个仓库向A、B两军营运送生活物资,已知甲仓库可调出生活物资100吨,乙仓库可调出生活物资80吨;A军营需生活物资70吨,B军营需生活物资110吨,两仓库到A、B两军营的路程和运费如下表:
路程(千米) | 运费(元/吨·千米) | |||
甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
A军营 | 20 | 15 | 12 | 12 |
B军营 | 25 | 20 | 10 | 8 |
设甲仓库运往A军营生活物资为x吨(x为整数),总运费为y(元).
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)若要使总运费不超过37160元,有几种运送生活物资方案?哪种运送方案总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
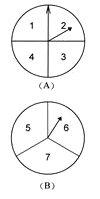
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() 的图象与
的图象与![]() 轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程
轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程![]() 的两个根,且A点坐标为(-6,0).
的两个根,且A点坐标为(-6,0).
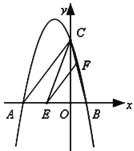
(1)求此二次函数的表达式;
(2)若点E是线段AB上的一个动点(与点A、B不重合),过点E作EF∥AC交BC于点F,连接CE.设AE的长为m,△CEF的面积为s,求S与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com