
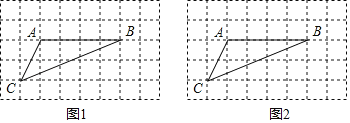
【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画出△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且四边形ACBD是中心对称图形;
(2)在图2中找一点E(点E在小正方形的顶点上),使tan∠AEB=2(AE<EB),且四边形ACEB的对边不平行,并直接写出图2中四边形ACEB的面积.
科目:初中数学 来源: 题型:
【题目】某地进行中考体育测试,规定测试项目分为必选项目与自选项目,男生自选项目是50米跑(A)、立定跳远(B)、引体向上(C)、1分钟跳绳(D),每个男生要在四个项目抽选两项进行测试.测试前,每个学生先抽一个,确定一个,再在所剩三个项目中再抽一个.张强同学的这四个项目中,他自认为50米跑更擅长.
(1)若张强先抽到立定跳远,然后再从剩下的项目中随机选择一项参加测试,则他刚好选中50米跑的概率是_______.
(2)若张强连续随机抽取两项,求其中抽中50米跑的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 随着互联网、移动终端的迅速发展,数字化阅读越来越普及. 公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
随着互联网、移动终端的迅速发展,数字化阅读越来越普及. 公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读”问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
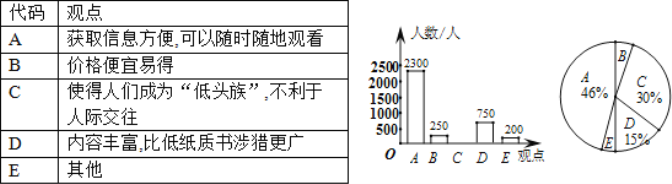
请根据统计图中提供的信息,解答下列问题:
(1)本次接受词查的总人数是______人,并将条形统计图补充完整;
(2)在扇形统计图中,观点E的百分比是_______,表示观点B的扇形的圆心角度数为______度.
(3)某市共有300万人,请根据以上调查结果估算该市持![]() 观点赞成数字化阅读的人数共有多少万人.
观点赞成数字化阅读的人数共有多少万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜种植农户购买白菜苗和西红柿苗共1000株,其中白菜苗每株3元,西红柿苗每株5元.已知该农户打算用不少于3600元但不多于3800元的资金购买两种蔬菜.
(1)求该农户可以购买白菜苗株数的最大值和最小值;
(2)该农户按(1)中购买白菜苗株数的最小值的方案购买两种蔬菜苗,经过农户的精心培育,两种蔬菜苗全成活.根据以往的数据分析,平均一株白菜苗可长成2千克白菜,平均一株西红柿苗可结3千克西红柿.农户计划采用直接销售和生态采摘销售两种方式进行销售,其中直接销售白菜的售价为每千克4元,直接销售西红柿的售价为每千克5元;生态采摘销售时两种蔬菜的售价一样,都比直接销售白菜的售价高![]() ,但生态采摘过程中会有
,但生态采摘过程中会有![]() 的损耗.当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时,该农户可获得8080元的利润.求
的损耗.当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时,该农户可获得8080元的利润.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
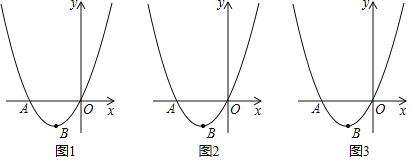
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于点A,顶点B的坐标为(﹣2,﹣2).
(1)求a,b的值;
(2)在y轴正半轴上取点C(0,4),在点A左侧抛物线上有一点P,连接PB交x轴于点D,连接CB交x轴于点F,当CB平分∠DCO时,求点P的坐标;
(3)在(2)的条件下,连接PC,在PB上有一点E,连接EC,若∠ECB=∠PDC,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
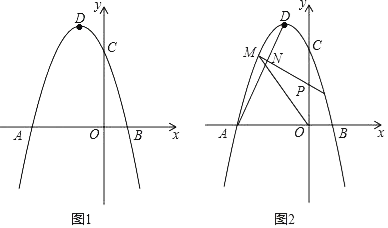
【题目】如图,抛物线的顶点D的坐标为(﹣1,4),抛物线与x轴相交于A.B两点(A在B的左侧),与y轴交于点C(0,3).
(1)求抛物线的表达式;
(2)如图1,已知点E(0,﹣3),在抛物线的对称轴上是否存在一点F,使得△CEF的周长最小,如果存在,求出点F的坐标;如果不存在,请说明理由;
(3)如图2,连接AD,若点P是线段OC上的一动点,过点P作线段AD的垂线,在第二象限分别与抛物线、线段AD相交于点M、N,当MN最大时,求△POM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线G:y=ax2﹣2ax+4(a≠0).
(1)当a=1时,
①抛物线G的对称轴为x= ;
②若在抛物线G上有两点(2,y1),(m,y2),且y2>y1,则m的取值范围是 ;
(2)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段AB恰有一个公共点,结合图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com