
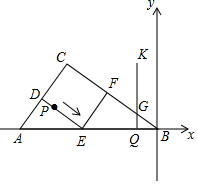
 ��ͼ����Rt��ABC�У���C=90�㣬AB=50��AC=30��D��E��F�ֱ���AC��AB��BC���е㣮��AB����ֱ��Ϊx�ᣬB��Ϊ����ԭ�㽨��ƽ��ֱ������ϵ����P�ӵ�D����������DE-EF-FC-CD��ÿ��7����λ���ȵ��ٶ������˶�����Q�ӵ�B������BA������ÿ��4����λ���ȵ��ٶ������˶�������Q������QK��AB��������BC-CA�ڵ�G����P��Qͬʱ����������P����һ�ܻص���Dʱֹͣ�˶�����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0����
��ͼ����Rt��ABC�У���C=90�㣬AB=50��AC=30��D��E��F�ֱ���AC��AB��BC���е㣮��AB����ֱ��Ϊx�ᣬB��Ϊ����ԭ�㽨��ƽ��ֱ������ϵ����P�ӵ�D����������DE-EF-FC-CD��ÿ��7����λ���ȵ��ٶ������˶�����Q�ӵ�B������BA������ÿ��4����λ���ȵ��ٶ������˶�������Q������QK��AB��������BC-CA�ڵ�G����P��Qͬʱ����������P����һ�ܻص���Dʱֹͣ�˶�����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ����t�루t��0�������� ��1������õ�C�͵�A�����꣬�������ߵĽ���ʽΪy=ax��x+50��������C�������������a��ֵ��
��2������DF������F��FH��AB������ΪH����֤���ı���CDEFΪ���Σ��ʴ˵�QK����DF���е���QKƽ���ı���CDEF�������
��3������P��EF��ʱ�������EQ��BQ�ij���Ȼ������EQ+BQ=EB�з�����⼴�ɣ�����P��FG��ʱ�������PB=5t��PF=7t-35��Ȼ������PB=PF+FB�з�����⼴�ɣ�
��4����Ϊ��P��ED�ϣ���P��EF�ϣ���P��CF����P��DC���������������P��PH��AB��Ȼ������PH=QG�з�����⼴�ɣ�
��� �⣺��1����Rt��ABC�У����ݹ��ɶ�����֪BC=40��
���C�����=-40��$\frac{4}{5}$=-32����C��������=40��$\frac{3}{5}$=24��
��C��-32��24����
��AB=50��
��A��-50��0����
�������ߵĽ���ʽΪy=ax��x+50��������C���������ã�18����-32��a=24�����a=-$\frac{1}{24}$��
�������ߵĽ���ʽΪy=-$\frac{1}{24}$x2-$\frac{25}{12}$x��
�ʴ�Ϊ��y=-$\frac{1}{24}$x2-$\frac{25}{12}$x��
��2���ܣ�
���ɣ���ͼ1��ʾ������DF������F��FH��AB������ΪH��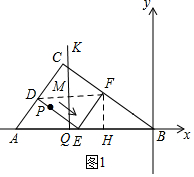
��D��F��E�ֱ�ΪAC��BC��AB���е㣬
��EF��DC��DE��CF��DF��AB��DF=25��
���ı���CDEFΪƽ���ı��Σ�
�֡ߡ�C=90�㣬
���ı���CDEFΪ���Σ�
�൱QK����DF���е�Mʱ��QK�Ѿ��η�Ϊ�����ȵ������֣�
��FM=QH��
��QH=12.5��
��BH=FBcos��B=20��$\frac{4}{5}$=16��
��QB=QH+HB=28.5
��t=$\frac{28.5}{4}$=7$\frac{1}{8}$��
��3����ͼ2��ʾ������P��EF��ʱ��
��EQ=$\frac{3}{5}$EP=$\frac{3}{5}$��7t-20����QB=4t��EQ+BQ=EB��
��$\frac{3}{5}$��7t-20��+4t=25����ã�t=4$\frac{21}{41}$��
��ͼ3��ʾ������P��FG��ʱ��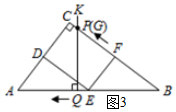
��QB=4t��
��PB=5t��
�֡�PF=7t-35��
��PB=PF+FB��
��5t=7t-35+20�����t=7$\frac{1}{2}$��
������������֪t��ֵΪ4$\frac{21}{41}$��7$\frac{1}{2}$��
��4����ͼ4��ʾ������P��ED��ʱ������P��PH��AB������ΪH��
��PH��GQ��
�൱PH=QGʱ���ı���PHQGΪƽ���ı��Σ�
���ʱPG��AB��
��PH=$\frac{3}{5}$��20-7t����GQ=$\frac{3}{4}$QB=3t��
��$\frac{3}{5}$��20-7t��=3t����ã�t=$\frac{5}{3}$��
��ͼ5��ʾ����2$\frac{6}{7}$��t��5ʱ����P��EF�ϣ�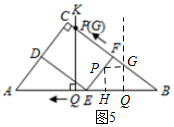
��PH=GQ��
��$\frac{4}{5}$��7t-20��=3t�����t=$\frac{80}{13}$��
��$\frac{80}{13}$��5��
����������������
����P��CF���˶�ʱ����G���P����BC�ϣ�PG��AB��ƽ�У�
��ͼ6��ʾ������P��CDʱ����PH��AB������ΪH��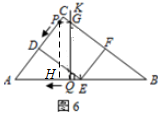
��AC=30��PC=7t-55��
��PH=$\frac{4}{5}$��85-7t����
�֡�QG=3t��
��$\frac{4}{5}$��85-7t��=3t�����t=7$\frac{39}{43}$��
������������t=$\frac{5}{3}$��t=7$\frac{39}{43}$ʱ��PG��AB��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ��ƽ�����ı��ε��������ʺ��ж������ɶ�����������Ǻ����Ķ��壬���������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
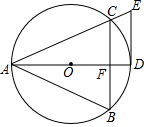 ��ͼ����OΪ����������ABC�����Բ��AB=AC��AD�ǡ�O��ֱ��������DE��AC���ӳ����ཻ�ڵ�E��
��ͼ����OΪ����������ABC�����Բ��AB=AC��AD�ǡ�O��ֱ��������DE��AC���ӳ����ཻ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
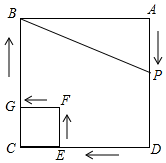 ��ͼ���߳�Ϊ4�Ĵ�������ABCD����һ���߳�Ϊ1��С������CEFG������P��ÿ��1cm���ٶȴӵ�A��������A��D��E��F��G��B��·���ƶ���εı������˶�����Bֹͣ��������A�͵�B�������ABP�����ΪS����P���˶�ʱ��Ϊt��
��ͼ���߳�Ϊ4�Ĵ�������ABCD����һ���߳�Ϊ1��С������CEFG������P��ÿ��1cm���ٶȴӵ�A��������A��D��E��F��G��B��·���ƶ���εı������˶�����Bֹͣ��������A�͵�B�������ABP�����ΪS����P���˶�ʱ��Ϊt���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
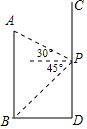 ��ͼ��AB��CD�ֱ��ʾ�������36�Ĵ�¥��С��ͬѧվ��CD��¥��P�����ڹ۲�AB��¥�ĵײ�B��ĸ���Ϊ45�㣬�۲�AB��¥�Ķ���A�������Ϊ30�㣮
��ͼ��AB��CD�ֱ��ʾ�������36�Ĵ�¥��С��ͬѧվ��CD��¥��P�����ڹ۲�AB��¥�ĵײ�B��ĸ���Ϊ45�㣬�۲�AB��¥�Ķ���A�������Ϊ30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
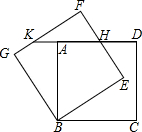 ��ͼ��������ABCD�Ƶ�B��ʱ����ת30���õ�������BEFG��EF��AD�ཻ�ڵ�H���ӳ�DA��GF�ڵ�K����������ABCD�߳�Ϊ$\sqrt{3}$����HD�ij�Ϊ$\sqrt{3}$-1��
��ͼ��������ABCD�Ƶ�B��ʱ����ת30���õ�������BEFG��EF��AD�ཻ�ڵ�H���ӳ�DA��GF�ڵ�K����������ABCD�߳�Ϊ$\sqrt{3}$����HD�ij�Ϊ$\sqrt{3}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com