
分析 (1)根据2阶6位循环数的定义,随便写出3个即可;结合数字的变化,找出变化规律“2阶6位循环数为任意的一个两位数×10101得出的”,根据10101是7的整数倍,即可得知任意一个2阶6位循环数能被7整除;
(2)结合(1)的规律可得出2阶4位循环数的变化规律“2阶4位循环数为任意的一个两位数×101得出的”,由101为质数可得出xy为13的倍数,结合x的取值范围即可得出y=3x.
解答 解:(1)依照2阶6位循环数的定义,随便写出3个2阶6位循环数:
131313;272727;868686.
任意一个2阶6位循环数能被7整除,理由如下:
结合数字的特点可得知:2阶6位循环数为任意的一个两位数×10101得出的.
∵10101÷7=1443,
∴任意一个2阶6位循环数能被7整除.
(2)结合(1)的规律可知:
2阶4位循环数为任意的一个两位数×101得出的.
∵101为质数,
∴xy为13的倍数,
又∵0<x<5,
∴y=3x.
当x=4时,y=3×4=12,4+1=5不符合题意,
∴0<x<4.
故y与x之间的函数关系为y=3x(0<x<4).
点评 本题考查了规律型中的数字的变化类,解题的关键是:(1)找出规律“2阶6位循环数为任意的一个两位数×10101得出的”;(2)找出规律“2阶4位循环数为任意的一个两位数×101得出的”.本题属于基础题,难度不大,解决该题型题目时,根据数字的特点找出变化规律是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
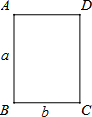 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙 S甲=S乙 | B. | V甲<V乙 S甲=S乙 | ||
| C. | V甲=V乙 S甲=S乙 | D. | V甲>V乙 S甲<S乙 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
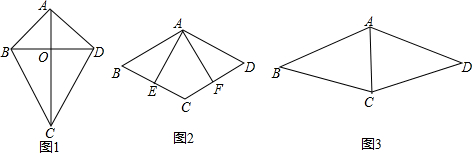
 如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com