
分析 首先把x的值代入1+x2进行化简,化成平方的形式,即可化简求值.
解答 解:1+x2=1+$\frac{1}{4}$(${2013}^{\frac{2}{n}}$+${2013}^{-\frac{2}{n}}$-2)=$\frac{1}{4}$(${2013}^{\frac{2}{n}}$+${2013}^{-\frac{2}{n}}$+2)=$\frac{1}{4}$(${2013}^{\frac{1}{n}}$+${2013}^{-\frac{1}{n}}$)2,
则原式=[$\frac{1}{2}$(${2013}^{\frac{1}{n}}$-${2013}^{-\frac{1}{n}}$)-$\frac{1}{2}$(${2013}^{\frac{1}{n}}$+${2013}^{-\frac{1}{n}}$)]n=(${2013}^{\frac{1}{n}}$)n=2013.
故答案是:2013.
点评 本题考查了二次根式的化简求值,正确对1+x2进行变形是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
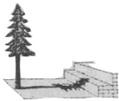 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )| A. | 6.93米 | B. | 8米 | C. | 11.8米 | D. | 12米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,茬四边形ABCD中,AD∥BC,E是BC的中点,AC平分∠BCD,且AC⊥AB,接DE,交AC于F.
如图,茬四边形ABCD中,AD∥BC,E是BC的中点,AC平分∠BCD,且AC⊥AB,接DE,交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.
如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图为8×9的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上.
如图为8×9的正方形网格,每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com