
·ÖĪö £Ø1£©øł¾ŻÖ±½ĒČż½ĒŠĪŠ±±ßÖŠĻߵĊŌÖŹ¼“æɽā¾öĪŹĢā£»
£Ø2£©øł¾ŻČż·ÖĻߵĶØŅ壬¼“æÉ»³öĶ¼ŠĪ£»
£Ø3£©×÷³öŠ±±ßÉĻµÄøߣ¬ŌŁ×÷³öĮ½øöŠ”Ö±½ĒČż½ĒŠĪµÄŠ±±ßµÄÖŠĻß¼“æÉ£»
£Ø4£©¼×”¢ŅŅĮ½øöĆüĢā¶¼ŹĒ¼ŁĆüĢā£»
½ā“š ½ā£ŗ£Ø1£©Ö±½ĒČż½ĒŠĪŠ±±ßÉĻÖŠĻßŅ»¶ØŹĒ2·ÖĻߣ®
£Ø2£©Čż·ÖĻßČēĶ¼ĖłŹ¾£¬×ó±ßĶ¼ÖŠ£¬Čż·ÖĻߵij¤ĪŖ$\sqrt{2}$£¬$\sqrt{3}$-1£»ÓŅ±ßĶ¼ÖŠČż·ÖĻߵij¤ĪŖ$\frac{2\sqrt{3}}{3}$£¬$\frac{\sqrt{3}}{3}$£»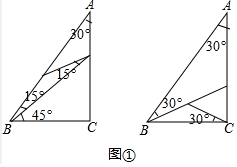
£Ø3£©ĖÄ·ÖĻßČēĶ¼ĖłŹ¾£¬£ØCDŹĒøߣ¬DE”¢DFŹĒÖŠĻߣ©
£Ø4£©¼×”¢ŅŅĮ½øöĆüĢā¶¼ŹĒ¼ŁĆüĢā£®¹ŹŃ”A£®
¹Ź“š°øĪŖA£®
µćĘĄ ±¾Ģāæ¼²éĆüĢāÓė¶ØĄķ”¢µČŃüČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢Ö±½ĒČż½ĒŠĪŠ±±ßÖŠĻß¶ØĄķµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£®


 »„¶ÆÓ¢ÓļĻµĮŠ“š°ø
»„¶ÆÓ¢ÓļĻµĮŠ“š°ø ĆūÅĘѧŠ£·Ö²ćÖÜÖܲāĻµĮŠ“š°ø
ĆūÅĘѧŠ£·Ö²ćÖÜÖܲāĻµĮŠ“š°ø »ĘøŌŗ£µķČ«³ĢÅąÓŲāŹŌ¾ķĻµĮŠ“š°ø
»ĘøŌŗ£µķČ«³ĢÅąÓŲāŹŌ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
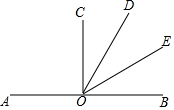 ČēĶ¼£¬OŹĒÖ±ĻßABÉĻŅ»µć£¬”ĻAOD=120”ć£¬”ĻAOC=90”ć£¬OEĘ½·Ö”ĻBOD£¬ŌņĶ¼ÖŠ±Ė“Ė»„²¹µÄ½Ē¹²ÓŠ£Ø””””£©
ČēĶ¼£¬OŹĒÖ±ĻßABÉĻŅ»µć£¬”ĻAOD=120”ć£¬”ĻAOC=90”ć£¬OEĘ½·Ö”ĻBOD£¬ŌņĶ¼ÖŠ±Ė“Ė»„²¹µÄ½Ē¹²ÓŠ£Ø””””£©| A£® | 4¶Ō | B£® | 5¶Ō | C£® | 6¶Ō | D£® | 7¶Ō |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ĄīĆ÷Ķ¬Ń§ŅŖÖ¤Ć÷ĆüĢā”°Čż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚČż½ĒŠĪµÄµŚČż±ß£¬²¢ĒŅµČÓŚµŚČż±ßµÄŅ»°ė”±£¬ĖūŅŃ¾»³öĮĖĶ¼ŠĪ£¬Š“³öŅŃÖŖŗĶĒóÖ¤£¬²¢ĒėÄć°ļÖśĖūŠ“³öÖ¤Ć÷¹ż³Ģ£®
ĄīĆ÷Ķ¬Ń§ŅŖÖ¤Ć÷ĆüĢā”°Čż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚČż½ĒŠĪµÄµŚČż±ß£¬²¢ĒŅµČÓŚµŚČż±ßµÄŅ»°ė”±£¬ĖūŅŃ¾»³öĮĖĶ¼ŠĪ£¬Š“³öŅŃÖŖŗĶĒóÖ¤£¬²¢ĒėÄć°ļÖśĖūŠ“³öÖ¤Ć÷¹ż³Ģ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
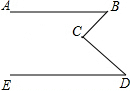 ČēĶ¼ĖłŹ¾£¬AB”ĪED£¬”ĻB=48”ć£¬”ĻD=42”ć£¬BC“¹Ö±ÓŚCDĀš£æČē¹ū“¹Ö±ĒėĖµĆ÷ĄķÓÉ£®
ČēĶ¼ĖłŹ¾£¬AB”ĪED£¬”ĻB=48”ć£¬”ĻD=42”ć£¬BC“¹Ö±ÓŚCDĀš£æČē¹ū“¹Ö±ĒėĖµĆ÷ĄķÓÉ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
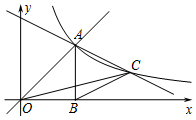 ČēĶ¼£¬Ö±Ļßy=xÓė·“Ė«ĒśĻßy=$\frac{k}{x}$£Øk£¾0£©ŌŚµŚŅ»ĻóĻŽ½»ÓŚµćA£¬AB”ĶxÖįÓŚB£Ø2£¬0£©£¬µćCŹĒĖ«ĒśĻßy=$\frac{k}{x}$£Øk£¾0£©Ķ¼ĻóÉĻŅ»¶Æµć£®
ČēĶ¼£¬Ö±Ļßy=xÓė·“Ė«ĒśĻßy=$\frac{k}{x}$£Øk£¾0£©ŌŚµŚŅ»ĻóĻŽ½»ÓŚµćA£¬AB”ĶxÖįÓŚB£Ø2£¬0£©£¬µćCŹĒĖ«ĒśĻßy=$\frac{k}{x}$£Øk£¾0£©Ķ¼ĻóÉĻŅ»¶Æµć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
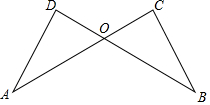 ŅŃÖŖ£ŗČēĶ¼£¬AD=BC£¬AC=BD£®ŹŌ²ĀĻėĻ߶ĪODÓėOCŹżĮæ¹ŲĻµ²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
ŅŃÖŖ£ŗČēĶ¼£¬AD=BC£¬AC=BD£®ŹŌ²ĀĻėĻ߶ĪODÓėOCŹżĮæ¹ŲĻµ²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com