
| 通话时间min | 2 | 3 | 6 | … |
| 通话费用/元 | 2.4 | 2.4 | 5.4 | … |
分析 (Ⅰ)根据从A地向B地打长途电话,通话时间不超过3mn收费2.4元,超过3min后每分加收1元计算即可解答;
(Ⅱ)分两种情况求函数解析式:当x≤3时;当x>3时,根据通话时间与收费标准,可得函数解析式;
(Ⅲ)根据通话时间与收费标准,可得函数解析式,根据函数值,可得相应自变量的值.
解答 解:(Ⅰ)根据通话时间不超过3mn收费2.4元,当通话时间为2min时,通话费为2.4元;
当通话时间6min时,通话费为2.4+(6-3)×1=5.4元;
故答案为:2.4,5.4.
(Ⅱ)当x≤3时,y=2.4,
当x>3时,y=2.4+(x-3)×1=x-0.6,
综上所述,y=$\left\{\begin{array}{l}{2.4(x≤3)}\\{x-0.6(x>3)}\end{array}\right.$.
(3)当y=10时,x-0.6=10,
解得x=10.6.
∵通话时间取整数,不足1min的通话时间按1min计费,
∴打一次电话最多可以通话10min,
答:有10元钱时,打一次电话最多可以通话10min.
点评 本题考查了分段函数,分类讨论是解题关键,利用通话时间与收费标准得出函数关系式.


科目:初中数学 来源: 题型:解答题
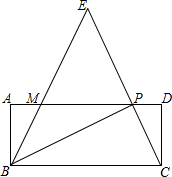 如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,
如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
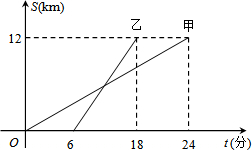 如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )
如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )| A. | 0.5千米 | B. | 1千米 | C. | 1.5千米 | D. | 2千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 名称及图形 几何点数 层数 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
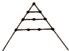 | 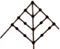 | 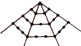 | 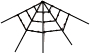 | |
| 第一层几何点数 | 1 | 1 | 1 | 1 |
| 第二层几何点数 | 2 | 3 | 4 | 5 |
| 第三层几何点数 | 3 | 5 | 7 | 9 |
| … | … | … | … | … |
| 第六层几何点数 | 6 | 11 | 16 | 21 |
| … | … | … | … | … |
| 第n层几何点数 | n | 2n-1 | 3n-2 | 4n-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;
已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com