
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论,其中正确结论是( ) 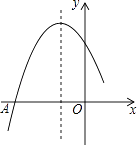
A.b2<4ac
B.2a+b=0
C.a+b+c>0
D.若点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,则y1<y2
,y2)为函数图象上的两点,则y1<y2
【答案】D
【解析】解:A、∵由函数图象可知抛物线与x轴有2个交点, ∴b2﹣4ac>0即b2>4ac,故本题选项错误;
B、∵对称轴为直线x=﹣1,
∴﹣ ![]() =﹣1,即2a﹣b=0,故本选项错误;
=﹣1,即2a﹣b=0,故本选项错误;
C、∵抛物线与x轴的交点A坐标为(﹣3,0)且对称轴为x=﹣1,
∴抛物线与x轴的另一交点为(1,0),
∴将(1,0)代入解析式可得,a+b+c=0,故本选项错误;
D、∵抛物线的对称轴是直线x=﹣1,抛物线的开口向下,
∴当x>﹣1时,y随x的增大而减小,
∵﹣1< ![]() <
< ![]() ,点B(
,点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,
,y2)为函数图象上的两点,
∴y1<y2 , 故本选项正确;
故选D.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2017的坐标为( )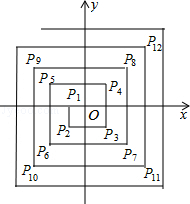
A.(504,﹣504)
B.(﹣504,504)
C.(﹣504,503)
D.(﹣505,504)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 纸片中,
纸片中,![]() cm,
cm,![]() cm。点
cm。点![]() 在
在![]() 边上,将
边上,将![]() 沿
沿![]() 折叠,得
折叠,得![]() ,连接
,连接![]() ,
, ![]() .
.
(1)当点![]() 落在
落在![]() 边上时,
边上时,![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的长;
的长;
(3)当![]() 分别满足下列条件时,求相应的
分别满足下列条件时,求相应的![]() 的长:
的长:
①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小军:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 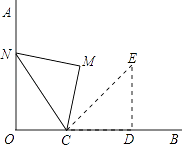
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图: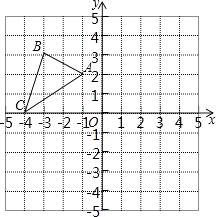
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出将△ABC绕点A逆时针旋转90°得到△AB2C2 ,
(3)△A1B1C1中顶点A1坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出 平面内不在同一条直线上的三点确定一个面,那么平面内的四点(任意三点均不在同一直线上),能否在同一个面上呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
(1)当C、D在线段AB的同侧时. 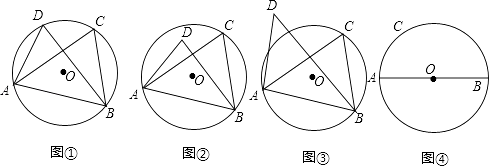
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 .
如图②,若点D在⊙O内,此时有∠ACB∠ADB;
如图③,若点D在⊙O外,此时有∠ACB∠ADB(填“=”、“>”、“<”)
由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形. 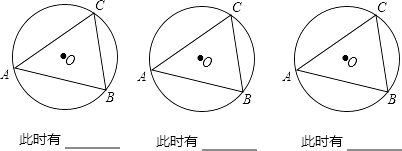
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线? 已知:如图,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB
作法:①连接CA、CB
②在CB上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB与M;
⑤连接D、M并延长,交⊙O于N,连接CN,则CN⊥AB.
请安上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)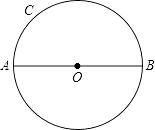
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是![]() cm,则BC的长是( )
cm,则BC的长是( )
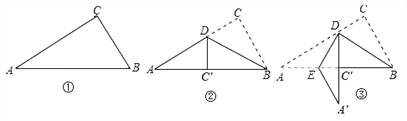
A. 3cm B. 4cm C. 5cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
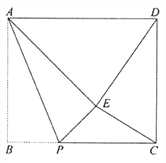
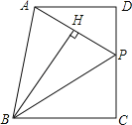
【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com