
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.
(1)如图1,若∠1=60°,求∠2,∠3的度数.

(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD请阅读下面的解答过程并填空(理由或数学式)
解:如图2,过点P作MN∥AB
则∠EPM=∠PEB(_______)
∵AB∥CD(已知)MN∥AB(作图)
∴MN∥CD(_______)
∴∠MPF=∠PFD (_______)
∴_____=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
②拓展应用,当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=_____度.
③当点P在图4的位置时,请直接写出∠EPF,∠PEB,∠PFD三个角之间关系_____.
【答案】(1)∠2=60°,∠3=60°;(2) 两直线平行,内错角相等 如果两条直线都和第三条直线平行,那么这两条直线也互相平行 两直线平行,内错角相等 ∠EPM+∠FPM 124 ∠EPF+∠PFD=∠PEB .
【解析】
(1)根据对顶角相等求∠2,根据两直线平行,同位角相等求∠3;
(2)①过点P作MN∥AB,根据平行线的性质得∠EPM=∠PEB,且有MN∥CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB+∠PFD.
②同①;
③利用平行线的性质和三角形的外角性质得到三个角之间的关系.
(1)∵∠2=∠1,∠1=60°
∴∠2=60°,
∵AB∥CD
∴∠3=∠1=60°;
(2)①如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
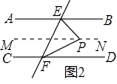
∵AB∥CD(已知),MN∥AB,
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD(两直线平行,内错角相等)
∴∠EPM+∠MPF=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD;
故答案为:两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠MPF;
②过点P作PM∥AB,如图3所示:
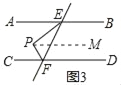
则∠PEB+∠EPM=180°,∠MPF+∠PFD=180°,
∴∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°,
即∠EPF+∠PEB+∠PFD=360°,
∴∠PFD=360°﹣80°﹣156°=124°;
故答案为:124;
③∠EPF+∠PFD=∠PEB.
故答案为:∠EPF+∠PFD=∠PEB.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知点A,B在数轴上对应的实数分别是a,b,其中a,b满足|a﹣2|+(b+1)2=0.
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程x﹣1=![]() x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)和(2)的条件下,点A,B,C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,设运动时间为t秒,试探究:随着时间t的变化,AB与BC满足怎样的数量关系?请写出相应的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )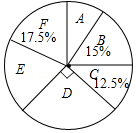
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (-3,-1) D. (-3,
) C. (-3,-1) D. (-3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.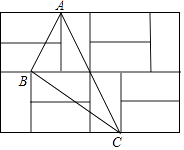
(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
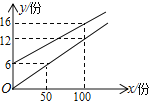
【题目】武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示
(1) 求甲、乙两种收费方式的函数关系式;
(2) 当印刷多少份学案时,两种印刷方式收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
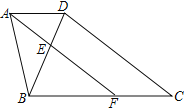
【题目】如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD
(1) 求AD的长;
(2) 若∠C=30°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD. 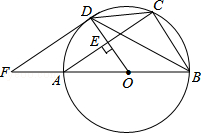
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com