
【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
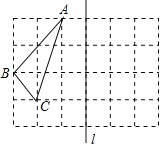
(1)△ABC的形状是 .
(2)利用网格线画△A′B′C′,使它与△ABC关于直线l对称.
(3)在直线l上求作点P使AP+CP的值最小,则AP+CP的最小值= .
【答案】(1)直角三角形;(2)见解析;(3)3![]() .
.
【解析】
(1)直接利用勾股定理以及勾股定理的逆定理,得出三边平方关系式分析得出答案;
(2)直接利用关于直线对称点的性质得出对应点位置,连线即得答案;
(3)直接利用对称点,两点之间线段最短的求最短路线方法得出答案.
(1)∵BC2=12+12=2,
AB2=22+22=8,
AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ABC是直角三角形;
故答案为:直角三角形;
(2)如图所示:作点对称,连线即得△A′B′C′即为所求;
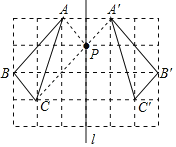
(3)根据两点之间线段最短,作出点A的对称点A′ ,连接A′C交直线l于点P,如图所示:点P即为所求,AP+CP的最小值=A′C=![]() =3
=3![]() .
.
故答案为:3![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,DE⊥AB于点E,连接OE,若DE=![]() ,BE=1,则∠AOE的度数是( )
,BE=1,则∠AOE的度数是( )
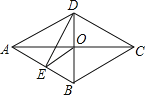
A.30°B.45°C.60°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在(1)问的条件下,平均每天获利不变,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
(3)写出每天总利润![]() 与降价
与降价![]() 元的函数关系式,为了使每天的利润最大,应降价多少元?
元的函数关系式,为了使每天的利润最大,应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分解因式![]() (直接写出结果);若
(直接写出结果);若![]() 是整数,则
是整数,则![]() 一定能被一个常数整除,这个常数的最大值是 .
一定能被一个常数整除,这个常数的最大值是 .
(2)阅读,并解决问题:
分解因式![]()
解:设![]() ,则原式
,则原式![]()
这样的解题方法叫做“换元法”,即当复杂的多项式中,某一部分重复出现时,我们用字母将其替换,从而简化这个多项式.换元法是一个重要的数学方法,不少问题能用换元法解决.请你用“换元法”对下列多项式进行因式分解:
①![]()
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,在△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
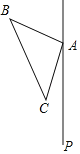
(1)依题意补全图形;
(2)若∠PAC=24°,求∠AEB的度数;
(3)连结CE,若AE=![]() ,CE=1,求BE长.
,CE=1,求BE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.
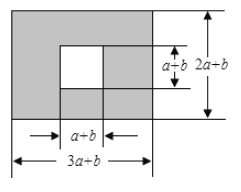
(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com