
ЎҫМвДҝЎҝДіөШОӘБЛ№ДАшҫУГсҪЪФјУГЛ®Ј¬ҫц¶ЁКөРРБҪј¶КХ·СЦЖЈ¬јҙГҝФВУГЛ®БҝІ»і¬№э12¶ЦЈЁә¬12¶ЦЈ©КұЈ¬Гҝ¶Ц°ҙХюё®І№МщУЕ»ЭјЫКХ·СЈ»ГҝФВі¬№э12¶ЦЈ¬і¬№эІҝ·ЦГҝ¶Ц°ҙКРіЎөчҪЪјЫКХ·СЈ¬РЎ»ЖјТ1ФВ·ЭУГЛ®24¶ЦЈ¬Ҫ»Л®·С42ФӘЈ®2ФВ·ЭУГЛ®20¶ЦЈ¬Ҫ»Л®·С32ФӘЈ®
ЈЁ1Ј©ЗуГҝ¶ЦЛ®өДХюё®І№МщУЕ»ЭјЫәНКРіЎөчҪЪјЫ·ЦұрКЗ¶аЙЩФӘЈ»
ЈЁ2Ј©ЙиГҝФВУГЛ®БҝОӘx¶ЦЈ¬УҰҪ»Л®·СОӘyФӘЈ¬РҙіцyУлxЦ®јдөДәҜКэ№ШПөКҪЈ»
ЈЁ3Ј©РЎ»ЖјТ3ФВ·ЭУГЛ®26¶ЦЈ¬ЛыјТУҰҪ»Л®·С¶аЙЩФӘЈҝ
Ўҫҙр°ёЎҝЈЁ1Ј©Гҝ¶ЦЛ®өДХюё®І№МщУЕ»ЭјЫОӘ1ФӘЈ¬КРіЎөчҪЪјЫОӘ2.5ФӘЈ®
ЈЁ2Ј©ЛщЗуәҜКэ№ШПөКҪОӘЈәy=![]() Ј®
Ј®
ЈЁ3Ј©РЎ»ЖјТИэФВ·ЭУҰҪ»Л®·С47ФӘЈ®
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©ЙиГҝ¶ЦЛ®өДХюё®І№МщУЕ»ЭјЫОӘaФӘЈ¬КРіЎөчҪЪјЫОӘbФӘЈ¬ёщҫЭМвТвБРіц·ҪіМЧйЈ¬ЗуҪвҙЛ·ҪіМЧйјҙҝЙЈ»
ЈЁ2Ј©ёщҫЭУГЛ®Бҝ·ЦұрЗуіцФЪБҪёцІ»Н¬өД·¶О§ДЪyУлxЦ®јдөДәҜКэ№ШПөЈ¬ЧўТвЧФұдБҝөДИЎЦө·¶О§Ј»
ЈЁ3Ј©ёщҫЭРЎ»ЖјТөДУГЛ®БҝЕР¶ПЖдФЩДДёц·¶О§ДЪЈ¬ҙъИлПаУҰөДәҜКэ№ШПөКҪЗуЦөјҙҝЙЈ®
ҪвЈәЈЁ1Ј©ЙиГҝ¶ЦЛ®өДХюё®І№МщУЕ»ЭјЫОӘaФӘЈ¬КРіЎөчҪЪјЫОӘbФӘЈ®
ёщҫЭМвТвөГ![]() Ј¬
Ј¬
ҪвөГЈә![]() Ј®
Ј®
ҙрЈәГҝ¶ЦЛ®өДХюё®І№МщУЕ»ЭјЫОӘ1ФӘЈ¬КРіЎөчҪЪјЫОӘ2.5ФӘЈ®
ЈЁ2Ј©ЎЯөұ0ЎЬxЎЬ12КұЈ¬y=xЈ»
өұxЈҫ12КұЈ¬y=12+ЈЁx©Ғ12Ј©ЎБ2.5=2.5x©Ғ18Ј¬
ЎаЛщЗуәҜКэ№ШПөКҪОӘЈәy=![]() Ј®
Ј®
ЈЁ3Ј©ЎЯx=26Јҫ12Ј¬
Ўа°Сx=26ҙъИлy=2.5x©Ғ18Ј¬өГЈәy=2.5ЎБ26©Ғ18=47ЈЁФӘЈ©Ј®
ҙрЈәРЎ»ЖјТИэФВ·ЭУҰҪ»Л®·С47ФӘЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»ёцКэөДЖҪ·ҪёщәНЛьөДБў·ҪёщПаөИЈ¬ФтХвёцКэКЗ_______Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ°СЕЧОпПЯy=x2+bx+cөДНјПуПтУТЖҪТЖ3ёцөҘО»Ј¬ФЩПтПВЖҪТЖ2ёцөҘО»Ј¬ЛщөГНјПуөДҪвОцКҪОӘy=x2©Ғ3x+5Ј¬ФтЈЁ Ј©
AЈ®b=3Ј¬c=7BЈ®b=6Ј¬c=3CЈ®b=©Ғ9Ј¬c=©Ғ5DЈ®b=©Ғ9Ј¬c=21
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПC=90ЎгЈ¬AC=6cmЈ¬BC=8cmЈ®өгPҙУAіц·ўЈ¬СШAB·ҪПтЈ¬ТФ2cm/sөДЛЩ¶ИПтөгBФЛ¶ҜЈ¬өгQҙУCіц·ўЈ¬СШCA·ҪПтЈ¬ТФ1cm/sөДЛЩ¶ИПтөгAФЛ¶ҜЈ»ИфБҪөгН¬Кұіц·ўЈ¬өұЖдЦРТ»өгөҪҙп¶ЛөгКұЈ¬БҪөгН¬КұНЈЦ№ФЛ¶ҜЈ¬ЙиФЛ¶ҜКұјдОӘtЈЁsЈ©Ј¬ЎчAPQөДГж»эОӘSЈЁcm2Ј©
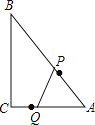
ЈЁ1Ј©t=2КұЈ¬ФтөгPөҪACөДҫаАлКЗ cmЈ¬S= cm2Ј»
ЈЁ2Ј©tОӘәОЦөКұЈ¬PQЎНABЈ»
ЈЁ3Ј©tОӘәОЦөКұЈ¬ЎчAPQКЗТФAQОӘөЧұЯөДөИСьИэҪЗРОЈ»
ЈЁ4Ј©ЗуSУлtЦ®јдөДәҜКэ№ШПөКҪЈ¬ІўЗуіцSөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪв·ҪіМЈә2x-3=3x-2Ј¬ХэИ·өДҙр°ёКЗЈЁ Ј©
A. x= 1 B. x= -1 C. x= 5 D. x= -5
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЎӘёц¶аұЯРОөДДЪҪЗәНКЗНвҪЗәНөД4ұ¶Ј¬ФтХвёц¶аұЯРОКЗ______ұЯРО.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ№ШУЪxөД·ҪіМЈә3x+m=2өДҪвТІКЗ·ҪіМЈәx- (1-x) =1өДҪвЈ¬ЗуmөДЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКөКэa<bЈ¬ФтПВБРҪбВЫЦРЈ¬І»ХэИ·өДКЗЈЁ Ј©
A. 4aЈј4b B. a+4<b+4 C. -4a<-4b D. a-4Јјb-4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИф№ШУЪxөД·ҪіМx2+3x+a=0УРТ»ёцёщОӘ©Ғ1Ј¬ФтБнТ»ёцёщОӘЈЁ Ј©
AЈ®©Ғ2 BЈ®2 CЈ®4 DЈ®©Ғ3
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com