
【题目】在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15, 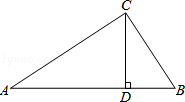
(1)求AB的长;
(2)求CD的长.
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F. 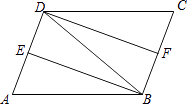
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索新知:
如图1,射线OC在![]() 的内部,图中共有3个角:
的内部,图中共有3个角:![]() ,
,![]() 和
和![]() ,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是
,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是![]() 的“巧分线”.
的“巧分线”.
(1)一个角的平分线______这个角的“巧分线”;![]() 填“是”或“不是”
填“是”或“不是”![]()
(2)如图2,若![]() ,且射线PQ是
,且射线PQ是![]() 的“巧分线”,则
的“巧分线”,则![]() ______;
______;![]() 用含
用含![]() 的代数式表示出所有可能的结果
的代数式表示出所有可能的结果![]()
深入研究:
如图2,若![]() ,且射线PQ绕点P从PN位置开始,以每秒
,且射线PQ绕点P从PN位置开始,以每秒![]() 的速度逆时针旋转,当PQ与PN成
的速度逆时针旋转,当PQ与PN成![]() 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是![]() 的“巧分线”;
的“巧分线”;
(4)若射线PM同时绕点P以每秒![]() 的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是
的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是![]() 的“巧分线”时t的值.
的“巧分线”时t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃. 
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科学技术协会为倡导青少年主动进行研究性学习,积极研究身边的科学问题,组织了以“体验、创新、成长”为主题的青少年科技创大赛,在层层选拔的基础上,所有推荐参赛学生分别获得了一、二、三等奖和纪念奖,工作人员根据获奖情况绘制成如图所示的两幅不完整的统计图,根据图中所给出的信息解答下列问题: 
(1)这次大赛获得三等奖的学生有多少人?
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示三等奖扇形的圆心角是多少度?
(4)若给所有推荐参赛学生每人发一张相同的卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出写有一等奖学生名字卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠DEC=60°,CE=2DE=4cm,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com