
本题中的图象,是表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程中路程y(千米)随时间x(小时)变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:

(1)分别求出表示轮船和快艇行驶过程中路程y(千米)随时间x(小时)变化的函数关系式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中行驶的速度分别是多少?
(3)快艇出发多长时间后追上轮船?
(1)y=20x,y=40x-80;(2)轮船行驶速度是20千米/时,快艇行驶速度是40千米/时;(3)2小时
【解析】
试题分析:(1)分别设出对应的函数关系式,再根据待定系数法即可求得结果;
(2)根据路程、速度、时间的关系结合图象中的数据特征即可求得结果;
(3)把(1)中的两个函数关系式组成方程组,求得方程组的解即可求得结果.
(1)设轮船行驶过程中路程y(千米)随时间x(小时)变化的函数关系式为y=kx.
由图象知当x=8时,y=160.
∴ 160=8k.∴ k=20.
∴ y=20x.
设快艇行驶过程中路程y(千米)随时间x(小时)变化的函数关系式为y=k1x+b1.
由图象知当x=2时,y=0.由图象知当x=6时,y=160.
∴  ,解得
,解得 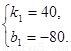
∴ y=40x-80.
(2)∵ 轮船航行8小时行驶160千米,
∴ 轮船行驶速度是160÷8=20(千米/时).
∵ 快艇航行4小时行驶160千米,
∴ 快艇行驶速度是160÷4=40(千米/时).
(3)解方程组  得
得

而 4-2=2.
答:快艇出发2小时后追上轮船.
考点:一次函数的应用
点评:解答本题的关键是读懂题意,找到量与量的关系,根据待定系数法正确求得一次函数关系式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 温度t/℃ | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
| 植物高度增长量l/mm | 1 | 24 | 39 | 49 | 49 | 41 | 25 | 1 |

查看答案和解析>>
科目:初中数学 来源: 题型:
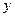 (厘米)与注水时间
(厘米)与注水时间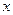 (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题: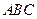 表示________槽中水的深度与注水时间的关系,线段
表示________槽中水的深度与注水时间的关系,线段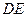 表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点
表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点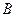 的纵坐标表示的实际意义是________________________________;
的纵坐标表示的实际意义是________________________________;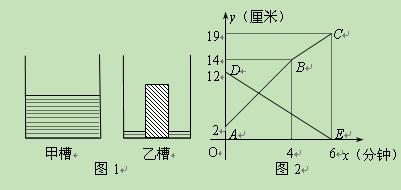
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省南通市幸福中学八年级上学期期中考试数学卷 题型:解答题
(本题12分)如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形块放其中(圆柱形铁块的下底面完全落在水槽底面上)现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示。根据图象提供的信息,解答下列问题:
【小题1】(1)图2中折线ABC表示 槽中的深度与注水时间之间的关系,线段DE表示 槽中的深度与注水时间之间的关系(以上两空选填“甲”、或“乙”),点B的纵坐标表示的实际意义是?
【小题2】(2)注水多长时间时,甲、乙两个水槽中的水的深度相同?
【小题3】(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
【小题4】(4)若乙槽中铁块的体积为112立方厘米(壁厚不计),求甲槽底面积(直接写结果)。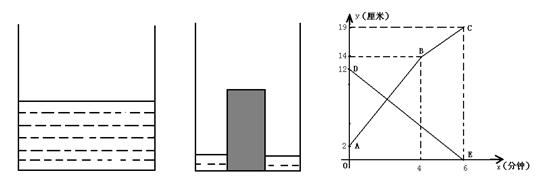
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷(带解析) 题型:解答题
本题中的图象,是表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程中路程y(千米)随时间x(小时)变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
(1)分别求出表示轮船和快艇行驶过程中路程y(千米)随时间x(小时)变化的函数关系式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中行驶的速度分别是多少?
(3)快艇出发多长时间后追上轮船?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com