
分析 首先计算乘方、开方和乘法,然后从左向右依次计算,求出算式(2$\sqrt{2}$-π)0-4cos60°+|$\sqrt{2}$-2|-$\sqrt{18}$的值是多少即可.
解答 解:(2$\sqrt{2}$-π)0-4cos60°+|$\sqrt{2}$-2|-$\sqrt{18}$
=1-4×$\frac{1}{2}$+2-$\sqrt{2}$-3$\sqrt{2}$
=1-2+2-4$\sqrt{2}$
=1-4$\sqrt{2}$
点评 此题主要考查了实数的运算,零指数幂、负整数指数幂和特殊角的三角函数值,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
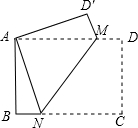 如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为$\frac{1}{3}$.
如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时$\frac{BN}{CN}$=$\frac{1}{3}$,则△AMD′的面积与△AMN的面积的比为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,-3),B(5,2),直线l2:y=k2x+2.
在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,-3),B(5,2),直线l2:y=k2x+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
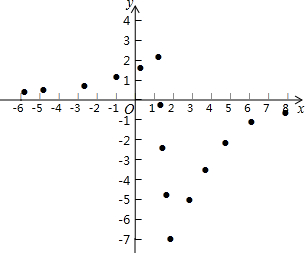 某“数学兴趣小组”根据学习函数的经验,对函数y=$\frac{-4x+6}{(x-2)^{2}}$的图象和性质进行了探究,探究过程如下,请补充完整:
某“数学兴趣小组”根据学习函数的经验,对函数y=$\frac{-4x+6}{(x-2)^{2}}$的图象和性质进行了探究,探究过程如下,请补充完整:查看答案和解析>>
科目:初中数学 来源:2017届山东省济宁市阶段教育学校统一招生考试数学模拟试卷(解析版) 题型:单选题
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
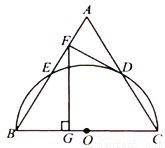
A. 4 B. 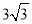 C. 6 D.
C. 6 D. 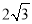
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省仙游县郊尾、枫亭五校教研小片区七年级下学期第一次月考数学试卷(解析版) 题型:单选题
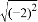 的值等于( )
的值等于( )
A. 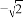 B. 一2 C. 2 D.
B. 一2 C. 2 D. 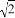
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com